Advertisements
Advertisements
प्रश्न
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s2?
उत्तर
It is given that:
Length of the pendulum, l = 5 m
Acceleration due to gravity, g = 9.8 ms-2
Acceleration due to gravity at the moon, g' = 1.67 ms-2
(a) Time period \[\left( T \right)\] is given by,
\[T = 2\pi\sqrt{\frac{l}{g}}\]
\[= 2\pi\sqrt{\frac{5}{9 . 8}}\]
\[ = 2\pi\sqrt{0 . 510} = 2\pi \left( 0 . 71 \right) s\]
i.e. the body will take 2 \[\pi\](0.7) seconds to complete an oscillation.
Now, frequency \[\left( f \right)\]is given by,
\[f = \frac{1}{T}\]
\[\therefore f = \frac{1}{2\pi\left( 0 . 71 \right)} \]
\[ = \frac{0 . 70}{\pi} Hz\]
(b) Let
\[g'\] be the value of acceleration due to gravity at moon. Time period of simple pendulum at moon \[\left( T' \right)\],is given as:
\[T' = 2\pi\sqrt{\left( \frac{l}{g'} \right)}\]
On substituting the respective values in the above formula, we get:
\[ = \frac{1}{2\pi}\sqrt{\frac{1 . 67}{5}} = \frac{1}{2\pi}\left( 0 . 577 \right)\]
\[ = \frac{1}{2\pi\sqrt{3}} Hz\]
APPEARS IN
संबंधित प्रश्न
The average displacement over a period of S.H.M. is ______.
(A = amplitude of S.H.M.)
Show variation of displacement, velocity, and acceleration with phase for a particle performing linear S.H.M. graphically, when it starts from the extreme position.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
Can a pendulum clock be used in an earth-satellite?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The displacement of a particle in simple harmonic motion in one time period is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
For a particle executing simple harmonic motion, the acceleration is proportional to
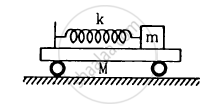
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on the surface of planet X such that the acceleration of the planet X is n times greater than the Earth is
Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
The displacement of a particle is represented by the equation `y = 3 cos (pi/4 - 2ωt)`. The motion of the particle is ______.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
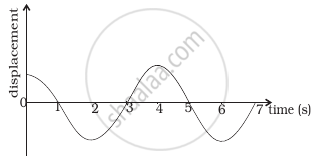
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
What is the ratio of maxmimum acceleration to the maximum velocity of a simple harmonic oscillator?
