Advertisements
Advertisements
प्रश्न
A small block oscillates back and forth on a smooth concave surface of radius R ib Figure . Find the time period of small oscillation.
उत्तर
The maximum tension in the string of an oscillating pendulum is double of the minimum tension. Find the angular amplitude.
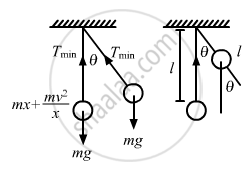
Let the speed of bob of the pendulum at an angle \[\theta\] be v.
Using the principle of conservation of energy between the mean and extreme positions, we get:
\[\frac{1}{2}\]mv2 − 0 = mgl(1 − cos θ)
v2 = 2gl(1 − cos θ) ...(1)
In a moving pendulum, the tension is maximum at the mean position, whereas it is minimum at the extreme position.
Maximum tension at the mean position is given by
Tmax = mg + 2mg(1 − cos θ)
Minimum tension at the extreme position is given by
Tmin = m g cosθ
According to the question,
Tmax = 2Tmin
⇒ mg + 2mg − 2m g cosθ = 2m g cosθ
⇒ 3mg = 4 mg cosθ
\[\Rightarrow \cos \theta = \frac{3}{4}\]
\[ \Rightarrow \theta = \cos^{- 1} \frac{3}{4}\]
APPEARS IN
संबंधित प्रश्न
Show variation of displacement, velocity, and acceleration with phase for a particle performing linear S.H.M. graphically, when it starts from the extreme position.
State the differential equation of linear simple harmonic motion.
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The distance moved by a particle in simple harmonic motion in one time period is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
A wall clock uses a vertical spring-mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
For a particle executing simple harmonic motion, the acceleration is proportional to
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
Write short notes on two springs connected in series.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
Which of the following expressions corresponds to simple harmonic motion along a straight line, where x is the displacement and a, b, and c are positive constants?
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
