Advertisements
Advertisements
प्रश्न
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
विकल्प
at correct rate
6 times faster
\[\sqrt{6}\] times faster
\[\sqrt{6}\] times slower
उत्तर
(d)\[\sqrt{6}\] times slower
The acceleration due to gravity at moon is g/6.
Time period of pendulum is given by,
\[T = 2\pi\sqrt{\frac{l}{g}}\]
Therefore, on moon, time period will be :
Tmoon = \[2\pi\sqrt{\frac{l}{g_{moon}}} = 2\pi\sqrt{\frac{l}{( \frac{g}{6})}} = \sqrt{6}(2\pi\sqrt{\frac{l}{g}}) = \sqrt{6}T\]
APPEARS IN
संबंधित प्रश्न
A particle in S.H.M. has a period of 2 seconds and amplitude of 10 cm. Calculate the acceleration when it is at 4 cm from its positive extreme position.
Show variation of displacement, velocity, and acceleration with phase for a particle performing linear S.H.M. graphically, when it starts from the extreme position.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses Pand Q equal number of times in a given time interval. Does it make you unhappy?
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?
A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
A wall clock uses a vertical spring-mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
Which of the following quantities are always positive in a simple harmonic motion?
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
For a particle executing simple harmonic motion, the acceleration is proportional to
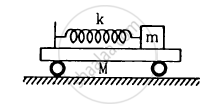
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45° with the X-axis. The two motions are given by x = x0 sin ωt and s = s0 sin ωt. Find the amplitude of the resultant motion.
The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on the surface of planet X such that the acceleration of the planet X is n times greater than the Earth is
A simple harmonic motion is given by, x = 2.4 sin ( 4πt). If distances are expressed in cm and time in seconds, the amplitude and frequency of S.H.M. are respectively,
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______
The displacement of a particle is represented by the equation `y = 3 cos (pi/4 - 2ωt)`. The motion of the particle is ______.
What is the ratio of maxmimum acceleration to the maximum velocity of a simple harmonic oscillator?
