Advertisements
Advertisements
प्रश्न
Which of the following quantities are always positive in a simple harmonic motion?
विकल्प
\[\vec{F} . \vec{a} .\]
\[\vec{v} . \vec{r} .\]
\[\vec{a} . \vec{r} .\]
\[\vec{F} . \vec{r} .\]
उत्तर
\[\vec{F} . \vec{a} \]
As the direction of force and acceleration are always same,
APPEARS IN
संबंधित प्रश्न
The average displacement over a period of S.H.M. is ______.
(A = amplitude of S.H.M.)
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses Pand Q equal number of times in a given time interval. Does it make you unhappy?
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
For a particle executing simple harmonic motion, the acceleration is proportional to
In a simple harmonic motion
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π/3 seconds to complete one oscillation. Find the acceleration of the elevator.
A simple pendulum fixed in a car has a time period of 4 seconds when the car is moving uniformly on a horizontal road. When the accelerator is pressed, the time period changes to 3.99 seconds. Making an approximate analysis, find the acceleration of the car.
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
Write short notes on two springs connected in parallel.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
The displacement of a particle is represented by the equation y = sin3ωt. The motion is ______.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
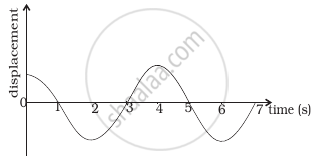
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.

