Advertisements
Advertisements
प्रश्न
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
उत्तर
The length of the simple pendulum is l.
Let x be the displacement of the simple pendulum..
(a)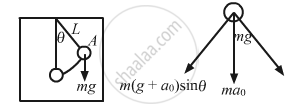
From the diagram, the driving forces f is given by,
f = m(g + a0)sinθ ...(1)
Acceleration (a) of the elevator is given by,
\[a = \frac{f}{m}\]
\[ = \left( g + a_0 \right)\sin\theta\]
\[ = \left( g + a_0 \right)\frac{x}{l} \left( \text{From the diagram } \sin\theta = \frac{x}{l} \right)_{}\]
[ when θ is very small, sin θ → θ = x/l]
\[\therefore a = \left( \frac{g + a_0}{l} \right)x\] ...(2)
As the acceleration is directly proportional to displacement, the pendulum executes S.H.M.
Comparing equation (2) with the expression a =\[\omega^2 x\],we get:
\[\omega^2 = \frac{g + a_0}{l}\]
Thus, time period of small oscillations when elevator is going upward(T) will be:
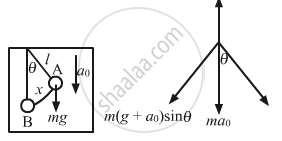
Driving force (F) is given by,
F = m(g − a0)sinθ
On comparing the above equation with the expression, F = ma,\[\text{Acceleration}, a = \left( g - a_0 \right) sin\theta = \frac{\left( g - a_0 \right)x}{l} = \omega^2 x\] \[\text{Time period of elevator when it is moving downward}\left( T' \right) \text{ is given by,} \]
\[T' = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{l}{g - a_0}}\]
(c) When the elevator moves with uniform velocity, i.e. a0 = 0,
For a simple pendulum, the driving force \[\left( F \right)\] is given by,
\[F = \frac{mgx}{l}\]
\[\text{Comparing the above equation with the expression, F = ma, we get: }\] \[a = \frac{gx}{l}\] \[ \Rightarrow \frac{x}{a} = \frac{l}{g}\] \[T = 2\pi\sqrt{\frac{\text{displacement}}{\text{Acceleration}}}\] \[ = 2\pi\sqrt{\frac{l}{g}}\]
APPEARS IN
संबंधित प्रश्न
Define phase of S.H.M.
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x
(b) a = –200x2
(c) a = –10x
(d) a = 100x3
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
Show variation of displacement, velocity, and acceleration with phase for a particle performing linear S.H.M. graphically, when it starts from the extreme position.
A particle executes simple harmonic motion. If you are told that its velocity at this instant is zero, can you say what is its displacement? If you are told that its velocity at this instant is maximum, can you say what is its displacement?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
For a particle executing simple harmonic motion, the acceleration is proportional to
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is ______.
- simple harmonic motion.
- non-periodic motion.
- periodic motion.
- periodic but not S.H.M.
A body having specific charge 8 µC/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally toward the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be ______ s.

The velocities of a particle in SHM at positions x1 and x2 are v1 and v2 respectively, its time period will be ______.
