Question

A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a₀(b) is going down with an acceleration a₀ and (c) is moving with a uniform velocity.

Answer 1

The length of the simple pendulum is l.
​Let x be the displacement of the simple pendulum..
(a)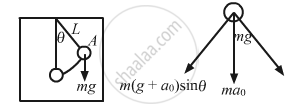

From the diagram, the driving forces f is given by,
f = m(g + a₀)sinθ                 ...(1)
Acceleration (a) of the elevator is given by,

\[a = \frac{f}{m}\] 

\[   = \left( g + a_0 \right)\sin\theta\] 

\[   = \left( g + a_0 \right)\frac{x}{l}       \left( \text{From  the  diagram } \sin\theta = \frac{x}{l} \right)_{}\]

[ when θ is very small, sin θ → θ = x/l]

\[\therefore a = \left( \frac{g + a_0}{l} \right)x\]  ...(2)

As the acceleration is directly proportional to displacement, the pendulum executes S.H.M.
Comparing equation (2) with the expression a =\[\omega^2 x\],we get:

\[\omega^2  = \frac{g + a_0}{l}\]

Thus, time period of small oscillations when elevator is going upward(T) will be:

\[T = 2\pi\sqrt{\frac{l}{g + a_0}}\]

When the elevator moves downwards with acceleration a₀,
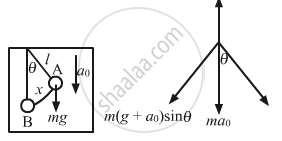
      Driving force (F) is given by,
      F = m(g − a₀)sinθ
On comparing the above equation with the expression, F = ma,\[\text{Acceleration},   a = \left( g - a_0 \right)  sin\theta = \frac{\left( g - a_0 \right)x}{l} =  \omega^2 x\] \[\text{Time  period  of  elevator  when  it  is  moving  downward}\left( T' \right) \text{ is  given  by,} \] 

\[T' = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{l}{g - a_0}}\]

(c) When the elevator moves with uniform velocity, i.e. a₀ = 0,
For a simple pendulum, the driving force \[\left( F \right)\] is given by,

\[F = \frac{mgx}{l}\] 

\[\text{Comparing  the  above  equation  with  the  expression,   F = ma,   we  get: }\] \[a = \frac{gx}{l}\] \[ \Rightarrow \frac{x}{a} = \frac{l}{g}\] \[T = 2\pi\sqrt{\frac{\text{displacement}}{\text{Acceleration}}}\] \[   = 2\pi\sqrt{\frac{l}{g}}\]