Advertisements
Advertisements
Question
Write short notes on two springs connected in series.
Advertisements
Solution
- When two or more springs are connected in series, we can replace (by removing) all the springs in series with an equivalent spring (effective spring) whose net effect is the same as if all the springs are in series connection.
- Given the value of individual spring constants k1, k2, k3, ... (known quantity), we can establish a mathematical relationship to find out an effective (or equivalent) spring constant ks (unknown quantity).
- For simplicity, let us consider only two springs whose spring constants are k1 and k2 and which can be attached to a mass m as shown in Figure.
- The results thus obtained can be generalised for any number of springs in series.
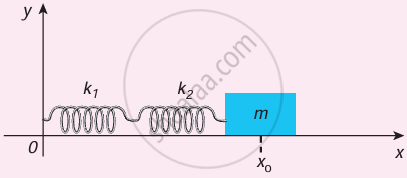
Springs are connected in series - Let F be the applied force towards right as shown in Figure. Since the spring constants for different springs are different and the connection points between them are not rigidly fixed, the strings can stretch in different lengths.
- Let x1 and x2 be the elongation of springs from their equilibrium position (un-stretched position) due to the applied force F. Then, the net displacement of the mass point is x = x1 + x2 ...(i)
- From Hooke’s law, the net force
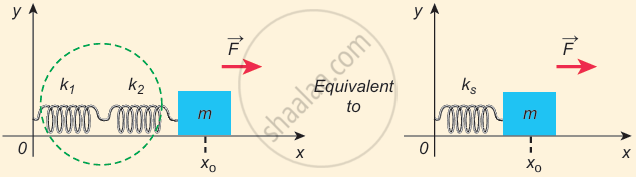
Effective spring constant in series connection
`F = -k_s(x_1 + x_2) => x_1 + x_2 = -F/K_s` ...(ii) - For springs in series connection
−k1 x1 = −k2 x2 = F
`=> x_1 = -F/k_1` and `x_2 = -F/k_2` ...(iii)
Therefore, substituting equation (iii) in equation (ii), the effective spring constant can be calculated as
`-F/k_1 - F/k_2 = -F/k_s`
`1/k_s = 1/k_1 + 1/k_2`
Or,
`k_s = (k_1k_2)/(k_1 + k_2)Nm^-1`
APPEARS IN
RELATED QUESTIONS
A particle in S.H.M. has a period of 2 seconds and amplitude of 10 cm. Calculate the acceleration when it is at 4 cm from its positive extreme position.
Show variation of displacement, velocity, and acceleration with phase for a particle performing linear S.H.M. graphically, when it starts from the extreme position.
State the differential equation of linear simple harmonic motion.
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
Which of the following will change the time period as they are taken to moon?
(a) A simple pendulum
(b) A physical pendulum
(c) A torsional pendulum
(d) A spring-mass system
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)
