Advertisements
Advertisements
प्रश्न
Write short notes on two springs connected in series.
उत्तर
- When two or more springs are connected in series, we can replace (by removing) all the springs in series with an equivalent spring (effective spring) whose net effect is the same as if all the springs are in series connection.
- Given the value of individual spring constants k1, k2, k3, ... (known quantity), we can establish a mathematical relationship to find out an effective (or equivalent) spring constant ks (unknown quantity).
- For simplicity, let us consider only two springs whose spring constants are k1 and k2 and which can be attached to a mass m as shown in Figure.
- The results thus obtained can be generalised for any number of springs in series.
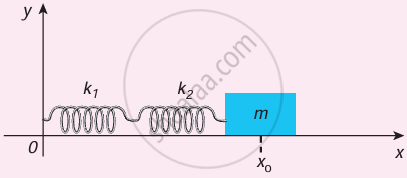
Springs are connected in series - Let F be the applied force towards right as shown in Figure. Since the spring constants for different springs are different and the connection points between them are not rigidly fixed, the strings can stretch in different lengths.
- Let x1 and x2 be the elongation of springs from their equilibrium position (un-stretched position) due to the applied force F. Then, the net displacement of the mass point is x = x1 + x2 ...(i)
- From Hooke’s law, the net force
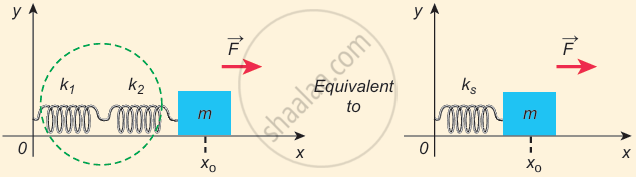
Effective spring constant in series connection
`F = -k_s(x_1 + x_2) => x_1 + x_2 = -F/K_s` ...(ii) - For springs in series connection
−k1 x1 = −k2 x2 = F
`=> x_1 = -F/k_1` and `x_2 = -F/k_2` ...(iii)
Therefore, substituting equation (iii) in equation (ii), the effective spring constant can be calculated as
`-F/k_1 - F/k_2 = -F/k_s`
`1/k_s = 1/k_1 + 1/k_2`
Or,
`k_s = (k_1k_2)/(k_1 + k_2)Nm^-1`
APPEARS IN
संबंधित प्रश्न
The energy of system in simple harmonic motion is given by \[E = \frac{1}{2}m \omega^2 A^2 .\] Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
A pendulum clock keeping correct time is taken to high altitudes,
A pendulum clock keeping correct time is taken to high altitudes,
A particle moves in a circular path with a continuously increasing speed. Its motion is
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
In a simple harmonic motion
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
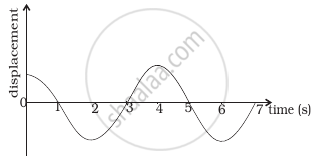
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.

