Advertisements
Advertisements
प्रश्न
A pendulum clock keeping correct time is taken to high altitudes,
पर्याय
it will keep correct time
its length should be increased to keep correct time
its length should be decreased to keep correct time
it cannot keep correct time even if the length is changed
उत्तर
its length should be decreased to keep correct time
Time period of pendulum,T =\[2\pi\sqrt{\frac{l}{g}}\]
At higher altitudes, the value of acceleration due to gravity decreases. Therefore, the length of the pendulum should be decreased to compensate for the decrease in the value of acceleration due to gravity.
APPEARS IN
संबंधित प्रश्न
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x
(b) a = –200x2
(c) a = –10x
(d) a = 100x3
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
A particle executes simple harmonic motion. If you are told that its velocity at this instant is zero, can you say what is its displacement? If you are told that its velocity at this instant is maximum, can you say what is its displacement?
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
Can a pendulum clock be used in an earth-satellite?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
The displacement of a particle in simple harmonic motion in one time period is
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
A pendulum clock keeping correct time is taken to high altitudes,
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
Which of the following will change the time period as they are taken to moon?
(a) A simple pendulum
(b) A physical pendulum
(c) A torsional pendulum
(d) A spring-mass system
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
A particle executing SHM crosses points A and B with the same velocity. Having taken 3 s in passing from A to B, it returns to B after another 3 s. The time period is ____________.
Write short notes on two springs connected in parallel.
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______
Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is ______.
- simple harmonic motion.
- non-periodic motion.
- periodic motion.
- periodic but not S.H.M.
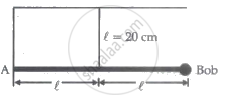
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)
Which of the following expressions corresponds to simple harmonic motion along a straight line, where x is the displacement and a, b, and c are positive constants?
