Advertisements
Advertisements
प्रश्न
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

उत्तर
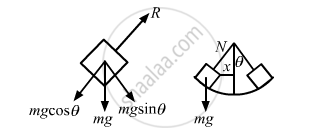
It is given that R is the radius of the concave surface.
Let N be the normal reaction force.
Driving force, F = mg sin θ
Comparing the expression for driving force with the expression, F = ma, we get:
Acceleration, a = g sin θ
Since the value of θ is very small,
∴ sin θ → θ
∴ Acceleration, a = gθ
Let x be the displacement of the body from mean position.
\[\therefore \theta = \frac{x}{R}\]
\[ \Rightarrow a = g\theta = g\left( \frac{x}{R} \right)\]
\[ \Rightarrow \left( \frac{a}{x} \right) = \left( \frac{g}{R} \right)\]
\[\Rightarrow a = x\frac{g}{R}\]
As acceleration is directly proportional to the displacement. Hence, the body will execute S.H.M.
Time period \[\left( T \right)\] is given by,
\[T = 2\pi\sqrt{\frac{\text { displacement }}{\text { Acceleration }}}\]
\[= 2\pi\sqrt{\frac{x}{gx/R}} = 2\pi\sqrt{\frac{R}{g}}\]
APPEARS IN
संबंधित प्रश्न
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate:
a) Angular frequency
b) frequency of vibration.
Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?
A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
A pendulum clock keeping correct time is taken to high altitudes,
A particle moves in a circular path with a continuously increasing speed. Its motion is
A particle moves in the X-Y plane according to the equation \[\overrightarrow{r} = \left( \overrightarrow{i} + 2 \overrightarrow{j} \right)A\cos\omega t .\]
The motion of the particle is
(a) on a straight line
(b) on an ellipse
(c) periodic
(d) simple harmonic
In a simple harmonic motion
(a) the maximum potential energy equals the maximum kinetic energy
(b) the minimum potential energy equals the minimum kinetic energy
(c) the minimum potential energy equals the maximum kinetic energy
(d) the maximum potential energy equals the minimum kinetic energy
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
Define the time period of simple harmonic motion.
What is an epoch?
The displacement of a particle is represented by the equation `y = 3 cos (pi/4 - 2ωt)`. The motion of the particle is ______.
Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is ______.
- simple harmonic motion.
- non-periodic motion.
- periodic motion.
- periodic but not S.H.M.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
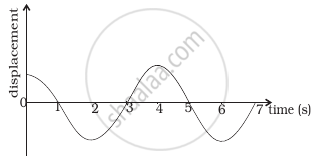
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
A body having specific charge 8 µC/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally toward the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be ______ s.

