Question

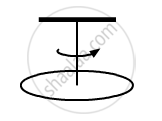
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?

Answer 1

It is given that:
Mass of disc = m
Radius of disc = r
The time period of torsional oscillations is T.
 Moment of inertia of the disc at the centre, I \[= \frac{m r^2}{2}\]

Time period of torsional pendulum\[\left( T \right)\] is given by,

\[T = 2\pi\sqrt{\frac{I}{k}}  \]

where I is the moment of inertia, and
           k is the torsional constant.

On substituting the value of moment of inertia in the expression for time period T, we have:

\[T = 2\pi\sqrt{\frac{m r^2}{2k}}\] 

\[\text { On  squaring  both  the  sides,   we  get: }\] 

\[ T^2  = 4 \pi^2 \frac{m r^2}{2k} = 2 \pi^2 \frac{m r^2}{k}\] 

\[ \Rightarrow 2 \pi^2 m r^2  = k T^2 \] 

\[ \Rightarrow k = \frac{2 \pi^2 m r^2}{T^2}\]