Question

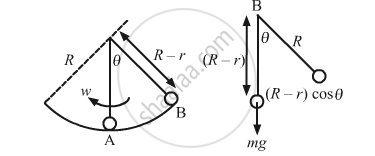
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.

Answer 1

Let ω be the angular velocity of the system about the point of suspension at any time.
Velocity of the ball rolling on a rough concave surface \[\left( v_C \right)\]  is given by,
v_c = (R − r)ω 
Also, v_c = rω₁  
where ω₁ is the rotational velocity of the sphere.

\[\Rightarrow  \omega_1  = \frac{v_c}{r} = \left( \frac{R - r}{r} \right)\omega                        \cdots\left( 1 \right)\]

As total energy of a particle in S.H.M. remains constant,

\[mg\left( R - r \right)  \left( 1 - \cos  \theta \right) + \frac{1}{2}m v_c^2  + \frac{1}{2}I \omega_1^2  = constant\] \[\text { Substituting  the  values  of   v_c   and }  \omega_1   \text { in  the  above  equation,   we  get: }\] \[mg  \left( R - r \right)  \left( 1 - \cos  \theta \right) + \frac{1}{2}m \left( R - r \right)^2    \omega^2  + \frac{1}{2}m r^2 \left( \frac{R - r}{r} \right) \omega^2  = \text { constant }       \left( \because I  = m r^2 \right)\] \[mg\left( R - r \right)  \left( 1 - \cos  \theta \right) + \frac{1}{2}m \left( R - r \right)^2    \omega^2  + \frac{1}{5}m r^2   \left( \frac{R - r}{r} \right) \omega^2  = \text { constant }\]\[ \Rightarrow g\left( R - r \right)  \left( 1 - \cos  \theta \right) +  \left( R - r \right)^2  \omega^2   \left[ \frac{1}{2} + \frac{1}{5} \right] = \text { constant }\]

Taking derivative on both sides, we get:

\[\text {g}\left( \text{R - r} \right)\text { sin }\theta\frac{\text{d}\theta}{\text{dt}} = \frac{7}{10} \left(\text{ R - r }\right)^2 2\omega\frac{d\omega}{\text{dt}}\] 

\[ \Rightarrow \text { g sin }\theta = 2 \times \left( \frac{7}{10} \right)\left(\text{ R - r }\right)\alpha    \left( \because a = \frac{\text{d}\omega}{\text{dt}} \right)\] 

\[ \Rightarrow \text{ g sin}\theta = \left( \frac{7}{5} \right)\left( \text{R - r} \right)\alpha\] 

\[ \Rightarrow \alpha = \frac{5\text{g sin }\theta}{7\left( \text{R - r} \right)}\] 

\[ = \frac{\text{5g}\theta}{7\left(\text{ R - r }\right)}\] 

\[ \therefore \frac{\alpha}{\theta} =  \omega^2  = \frac{\text{5g}}{7\left( \text{R - r} \right)} = \text { constant }\]

Therefore, the motion is S.H.M.

\[\omega = \sqrt{\frac{5g}{7\left( R - r \right)}}\] 

\[\text { Time  period  is  given  by, } \] 

\[ \Rightarrow T = 2\pi\sqrt{\frac{7\left( R - r \right)}{5g}}\]