Advertisements
Advertisements
प्रश्न
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
उत्तर
It is given that:
Length of the pendulum, l = 40 cm = 0.4 m
Radius of the earth, R = 6400 km
Acceleration due to gravity on the earth's surface, `g = 9.8 "ms"^(- 2)`
Let
\[g'\] be the acceleration due to gravity at a depth of 1600 km from the surface of the earth.
Its value is given by,
\[g' = g\left( 1 - \frac{d}{R} \right)\] \[\text{where d is the depth from the earth surfce, }\] \[\text { R is the radius of earth, and }\]
\[\text {g is acceleration due to gravity .}\]
\[\text{ On substituting the respective values, we get: }\] \[ g' = 9 . 8\left( 1 - \frac{1600}{6400} \right)\]
\[= 9 . 8\left( 1 - \frac{1}{4} \right)\]
\[= 9 . 8 \times \left( \frac{3}{4} \right) = 7 . 35 {\text{ms}}^{- 2}\]
Time period is given as,
\[\Rightarrow T = 2\pi\sqrt{\left( \frac{0 . 4}{7 . 35} \right)}\]
\[ \Rightarrow T = 2 \times 3 . 14 \times 0 . 23\]
\[ = 1 . 465 \approx 1 . 47 s\]
APPEARS IN
संबंधित प्रश्न
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on a horizontal plane move in a sample harmonic motion?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
The distance moved by a particle in simple harmonic motion in one time period is
A pendulum clock keeping correct time is taken to high altitudes,
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
A particle moves in the X-Y plane according to the equation \[\overrightarrow{r} = \left( \overrightarrow{i} + 2 \overrightarrow{j} \right)A\cos\omega t .\]
The motion of the particle is
(a) on a straight line
(b) on an ellipse
(c) periodic
(d) simple harmonic
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be __________.
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
Describe Simple Harmonic Motion as a projection of uniform circular motion.
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.

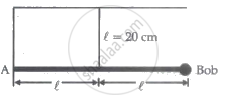
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)