Advertisements
Advertisements
प्रश्न
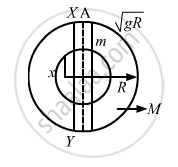
Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
उत्तर
Given:
Radius of the earth is R.
Let M be the total mass of the earth and \[\rho\] be the density.
Let mass of the part of earth having radius x be M.
\[\therefore \frac{M'}{M} = \frac{\rho \times \frac{4}{3}\pi x^3}{\rho \times \frac{4}{3}\pi R^3} = \frac{x^3}{R^3}\]
\[ \Rightarrow M' = \frac{M x^3}{R^3}\]
Force on the particle is calculated as,
\[F_x = \frac{GM'm}{x^2}\]
\[ = \frac{GMm}{R^3}x \ldots\left( 1 \right)\]
Now, acceleration \[\left( a_x \right)\] of mass M' at that position is given by,
\[a_x = \frac{GM}{R^3}x\]
\[ \Rightarrow \frac{a_x}{x} = \omega^2 = \frac{GM}{R^3} = \frac{g}{R} \left( \because g = \frac{GM}{R^2} \right)\]
\[\text{So, Time period of oscillation ,} T = 2\pi\sqrt{\left( \frac{R}{g} \right)}\]
(a) Velocity-displacement equation in S.H.M is written as,
\[V = \omega\sqrt{\left( A^2 - y^2 \right)} \]
where, A is the amplitude; and y is the displacement .
When the particle is at y = R,
The velocity of the particle is \[\sqrt{gR}\] and \[\omega = \sqrt{\frac{g}{R}}\]
On substituting these values in the velocity-displacement equation, we get:
\[\sqrt{gR} = \sqrt{\frac{g}{R}}\sqrt{A^2 - R^2} \]
\[ \Rightarrow R^2 = A^2 - R^2 \]
\[ \Rightarrow A = \sqrt{2R}\]
Let t1 and t2 be the time taken by the particle to reach the positions X and Y.
Now, phase of the particle at point X will be greater than \[\frac{\pi}{2}\] but less than \[\pi\]
Also, the phase of the particle on reaching Y will be greater than \[\pi\] but less than \[\frac{3\pi}{2}\]
Displacement-time relation is given by,
y = A sin ωt
Substituting y = R and A =\[\sqrt{2R}\] , in the above relation , we get :
\[R = \sqrt{2}R \sin \omega t_1\]
\[\Rightarrow \omega t_1 = \frac{3\pi}{4}\]
Also,
\[R = \sqrt{2}R \sin \omega t_2\]
\[\Rightarrow \omega t_2 = \frac{5\pi}{4}\]
\[\text{So}, \omega\left( t_2 - t_1 \right) = \frac{\pi}{2}\]
\[ \Rightarrow t_2 - t_1 = \frac{\pi}{2\omega} = \frac{\pi}{2\left( \sqrt{\frac{g}{R}} \right)}\]
Time taken by the particle to travel from X to Y:
Using the principle of conservation of energy, we get:
Change in P.E. = Gain in K.E.
\[\Rightarrow \frac{GMm}{R} - \frac{GMm}{2R} = \frac{1}{2}m v^2 \]
\[ \Rightarrow v = \sqrt{\left( gR \right)}\]
As the velocity is same as that at X, the body will take the same time to travel XY.
(c) The body is projected vertically upwards from the point X with a velocity \[\sqrt{gR}\].Its velocity becomes zero as it reaches the highest point.
The velocity of the body as it reaches X again will be,
\[v = \sqrt{\left( gR \right)}\]
Hence, the body will take same time i.e.
APPEARS IN
संबंधित प्रश्न
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
A pendulum clock gives correct time at the equator. Will it gain time or loose time as it is taken to the poles?
Can a pendulum clock be used in an earth-satellite?
The displacement of a particle in simple harmonic motion in one time period is
A wall clock uses a vertical spring-mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
A pendulum clock keeping correct time is taken to high altitudes,
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
In a simple harmonic motion
A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
What is an epoch?
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.

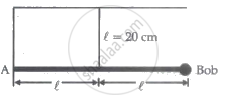
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)