Advertisements
Advertisements
प्रश्न
Can a pendulum clock be used in an earth-satellite?
उत्तर
No. According to the relation :
APPEARS IN
संबंधित प्रश्न
State the differential equation of linear simple harmonic motion.
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
A pendulum clock keeping correct time is taken to high altitudes,
A pendulum clock keeping correct time is taken to high altitudes,
For a particle executing simple harmonic motion, the acceleration is proportional to
An object is released from rest. The time it takes to fall through a distance h and the speed of the object as it falls through this distance are measured with a pendulum clock. The entire apparatus is taken on the moon and the experiment is repeated
(a) the measured times are same
(b) the measured speeds are same
(c) the actual times in the fall are equal
(d) the actual speeds are equal
A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
A simple pendulum fixed in a car has a time period of 4 seconds when the car is moving uniformly on a horizontal road. When the accelerator is pressed, the time period changes to 3.99 seconds. Making an approximate analysis, find the acceleration of the car.
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
A particle executing SHM crosses points A and B with the same velocity. Having taken 3 s in passing from A to B, it returns to B after another 3 s. The time period is ____________.
Write short notes on two springs connected in series.
What is meant by simple harmonic oscillation? Give examples and explain why every simple harmonic motion is a periodic motion whereas the converse need not be true.
The displacement of a particle is represented by the equation `y = 3 cos (pi/4 - 2ωt)`. The motion of the particle is ______.
What is the ratio of maxmimum acceleration to the maximum velocity of a simple harmonic oscillator?
A body having specific charge 8 µC/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally toward the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be ______ s.

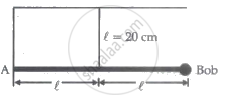
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)