Advertisements
Advertisements
प्रश्न
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
उत्तर
Let T1 be the time period of pendulum clock at a place where acceleration due to gravity \[\left( g_1 \right)\] is 9.8 ms−2.
Let T1 = 2 s
`g_1 = 9.8"ms"^(-2)`
Let T2 be the time period at the place where the pendulum clock loses 24 seconds during 24 hours.
Acceleration due to gravity at this place is \[\left( g_2 \right)\]
\[T_2 = \frac{24 \times 3600}{\frac{\left( 24 \times 3600 - 24 \right)}{2}}\]
\[ = 2 \times \frac{3600}{3599}\]
As
\[T \propto \frac{1}{\sqrt{g}}\]
\[\therefore \frac{T_1}{T_2} = \sqrt{\left( \frac{g_2}{g_1} \right)}\]
\[\Rightarrow \frac{g_2}{g_1} = \left( \frac{T_1}{T_2} \right)^2 \]
\[ \Rightarrow g_2 = \left( 9 . 8 \right) \left( \frac{3599}{3600} \right)^2 \]
\[ = 9 . 795 \text { m/ s}^2\]
APPEARS IN
संबंधित प्रश्न
In a damped harmonic oscillator, periodic oscillations have _______ amplitude.
(A) gradually increasing
(B) suddenly increasing
(C) suddenly decreasing
(D) gradually decreasing
Show variation of displacement, velocity, and acceleration with phase for a particle performing linear S.H.M. graphically, when it starts from the extreme position.
State the differential equation of linear simple harmonic motion.
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on a horizontal plane move in a sample harmonic motion?
Figure represents two simple harmonic motions.
The parameter which has different values in the two motions is

A pendulum clock keeping correct time is taken to high altitudes,
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
A particle moves in the X-Y plane according to the equation \[\overrightarrow{r} = \left( \overrightarrow{i} + 2 \overrightarrow{j} \right)A\cos\omega t .\]
The motion of the particle is
(a) on a straight line
(b) on an ellipse
(c) periodic
(d) simple harmonic
A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
Which of the following will change the time period as they are taken to moon?
(a) A simple pendulum
(b) A physical pendulum
(c) A torsional pendulum
(d) A spring-mass system
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
Define the frequency of simple harmonic motion.
What is an epoch?
Describe Simple Harmonic Motion as a projection of uniform circular motion.
The displacement of a particle is represented by the equation y = sin3ωt. The motion is ______.
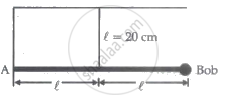
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
