Question

Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.

Answer 1

If \[\rho\]  is the density of the earth, then mass of the earth \[\left( M \right)\] is given by,

\[M = \frac{4}{3}\pi R^3 \rho\] 

\[\text {Similarly,   mass}  \left( M' \right) \text{ of  the  part  of  earth  having  radius } \left( x \right)\text{  is  given  by, } \] \[M' = \frac{4}{3}\pi {x_1}^3 \rho\] 

\[M' = \left( \frac{M}{R^3} \right) {x_1}^3\]

(a) Let F be the gravitational force exerted by the earth on the particle of mass m. Then, its value is given by,

\[F = \frac{GM'm}{x_1^2}\] 

\[\text {Substituting  the  value  of  M'  in  the  above  equation,   we  get: }\] 

\[F = \frac{GMm}{R^3}\frac{x_1^3}{x_1^2}\] 

\[   = \frac{GMm}{R^3} x_1  = \frac{GMm}{R^3}\sqrt{x^2 + \left( \frac{R^2}{4} \right)}\]

(b)

\[F_y  = Fcos\theta\] 

\[     = \frac{GMm x_1}{R^3}\frac{x}{x_1} = \frac{GMmx}{R^3}\] 

\[ F_x  = F\sin  \theta\] 

\[     = \frac{GMm x_1}{R^3}\frac{R}{2 x_1} = \frac{GMm}{2 R^2}\]

 (c)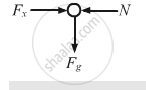

\[F_x  = \frac{GMm}{R^2}\]

\[\because\] Normal force exerted by the wall N = F_x
(d)The resultant force is \[\frac{GMmx}{R^3}\]

(e) Acceleration = Driving force/mass 

\[= \frac{GMmx}{R^3 m}\] 

\[ = \frac{GMx}{R^3}\]

\[\Rightarrow\] a \[\propto\]  x      (the body executes S.H.M.)
 \[\frac{a}{x} =  \omega^2  = \frac{GM}{R^3}\] 

\[ \Rightarrow \omega = \sqrt{\frac{Gm}{R^3}}\] 

\[ \Rightarrow T = 2\pi\sqrt{\frac{R^3}{GM}}\]