Advertisements
Advertisements
Question
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
Advertisements
Solution
If \[\rho\] is the density of the earth, then mass of the earth \[\left( M \right)\] is given by,
\[M = \frac{4}{3}\pi R^3 \rho\]
\[\text {Similarly, mass} \left( M' \right) \text{ of the part of earth having radius } \left( x \right)\text{ is given by, } \] \[M' = \frac{4}{3}\pi {x_1}^3 \rho\]
\[M' = \left( \frac{M}{R^3} \right) {x_1}^3\]
(a) Let F be the gravitational force exerted by the earth on the particle of mass m. Then, its value is given by,
\[F = \frac{GM'm}{x_1^2}\]
\[\text {Substituting the value of M' in the above equation, we get: }\]
\[F = \frac{GMm}{R^3}\frac{x_1^3}{x_1^2}\]
\[ = \frac{GMm}{R^3} x_1 = \frac{GMm}{R^3}\sqrt{x^2 + \left( \frac{R^2}{4} \right)}\]
(b)
\[F_y = Fcos\theta\]
\[ = \frac{GMm x_1}{R^3}\frac{x}{x_1} = \frac{GMmx}{R^3}\]
\[ F_x = F\sin \theta\]
\[ = \frac{GMm x_1}{R^3}\frac{R}{2 x_1} = \frac{GMm}{2 R^2}\]
(c)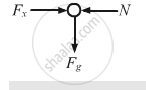 
\[F_x = \frac{GMm}{R^2}\]
\[\because\] Normal force exerted by the wall N = Fx
(d)The resultant force is \[\frac{GMmx}{R^3}\]
(e) Acceleration = Driving force/mass
\[= \frac{GMmx}{R^3 m}\]
\[ = \frac{GMx}{R^3}\]
\[\Rightarrow\] a \[\propto\] x (the body executes S.H.M.)
\[\frac{a}{x} = \omega^2 = \frac{GM}{R^3}\]
\[ \Rightarrow \omega = \sqrt{\frac{Gm}{R^3}}\]
\[ \Rightarrow T = 2\pi\sqrt{\frac{R^3}{GM}}\]
APPEARS IN
RELATED QUESTIONS
In a damped harmonic oscillator, periodic oscillations have _______ amplitude.
(A) gradually increasing
(B) suddenly increasing
(C) suddenly decreasing
(D) gradually decreasing
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
A wall clock uses a vertical spring-mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
Which of the following quantities are always positive in a simple harmonic motion?
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
Define the time period of simple harmonic motion.
Write short notes on two springs connected in series.
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)
Which of the following expressions corresponds to simple harmonic motion along a straight line, where x is the displacement and a, b, and c are positive constants?
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
If x = `5 sin (pi t + pi/3) m` represents the motion of a particle executing simple harmonic motion, the amplitude and time period of motion, respectively, are ______.
