Advertisements
Advertisements
Question
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
Solution
It is given that the length of the rod is l.
Let point A be the suspension point and point B be the centre of gravity.
Separation between the point of suspension and the centre of mass, l' = \[\frac{l}{2}\]
Also, h =\[\frac{l}{2}\]
Using parallel axis theorem, the moment of inertia about A is given as,
\[I = I_{CG} + m h^2 \]
\[ = \frac{m l^2}{12} + \frac{m l^2}{4} = \frac{m l^2}{3}\]
\[\text { the time period }\left( T \right) \text { is given by, }\]
\[T = 2\pi\sqrt{\frac{I}{mgl'}} = 2\pi\sqrt{\frac{I}{mg\frac{l}{2}}}\]
\[ = 2\pi\sqrt{\frac{2m l^2}{3mgl}} = 2\pi\sqrt{\frac{2l}{3g}}\]
Let T' be the time period of simple pendulum of length x.
Time Period \[(T')\] is given by ,\[T' = 2\pi\sqrt{\left( \frac{x}{g} \right)}\] \[\text { As the time period of the simple pendulum is equal to the time period of the rod,} \] \[T' = T\]
\[ \Rightarrow \frac{2l}{3g} = \frac{x}{g}\]
\[ \Rightarrow x = \frac{2l}{3}\]
APPEARS IN
RELATED QUESTIONS
A particle in S.H.M. has a period of 2 seconds and amplitude of 10 cm. Calculate the acceleration when it is at 4 cm from its positive extreme position.
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
A particle executes simple harmonic motion. If you are told that its velocity at this instant is zero, can you say what is its displacement? If you are told that its velocity at this instant is maximum, can you say what is its displacement?
A block of known mass is suspended from a fixed support through a light spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
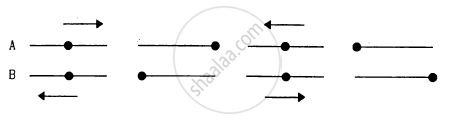
Figure represents two simple harmonic motions.
The parameter which has different values in the two motions is
A wall clock uses a vertical spring-mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
A particle moves in a circular path with a continuously increasing speed. Its motion is
Which of the following quantities are always positive in a simple harmonic motion?
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
Write short notes on two springs connected in parallel.
State the laws of the simple pendulum?
A simple harmonic motion is given by, x = 2.4 sin ( 4πt). If distances are expressed in cm and time in seconds, the amplitude and frequency of S.H.M. are respectively,
