Advertisements
Advertisements
Question
A block of known mass is suspended from a fixed support through a light spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
Advertisements
Solution
Yes.
Time period of a spring mass system is given by,\[T = 2\pi\sqrt{\frac{m}{k}}\] ...(1) where m is mass of the block, and
k is the spring constant
Time period is also given by the relation,
\[T = 2\pi\sqrt{\frac{x_0}{g}}\] ...(2)
where, x0 is extension of the spring, and
g is acceleration due to gravity
From the equations (1) and (2), we have :
\[mg = k x_0\]
\[\Rightarrow k = \frac{mg}{x_0}\]
Substituting the value of k in the above equation, we get:
Thus, we can find the time period if the value of extension x0 is known.
APPEARS IN
RELATED QUESTIONS
The average displacement over a period of S.H.M. is ______.
(A = amplitude of S.H.M.)
Define phase of S.H.M.
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x
(b) a = –200x2
(c) a = –10x
(d) a = 100x3
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate:
a) Angular frequency
b) frequency of vibration.
Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?
The displacement of a particle in simple harmonic motion in one time period is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
Which of the following quantities are always positive in a simple harmonic motion?
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be __________.
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
Write short notes on two springs connected in series.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
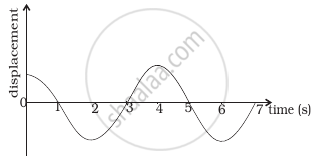
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.
