Advertisements
Advertisements
Question
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.
Advertisements
Solution
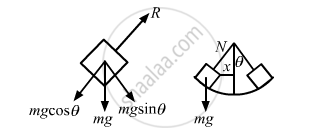
It is given that R is the radius of the concave surface.
Let N be the normal reaction force.
Driving force, F = mg sin θ
Comparing the expression for driving force with the expression, F = ma, we get:
Acceleration, a = g sin θ
Since the value of θ is very small,
∴ sin θ → θ
∴ Acceleration, a = gθ
Let x be the displacement of the body from mean position.
\[\therefore \theta = \frac{x}{R}\]
\[ \Rightarrow a = g\theta = g\left( \frac{x}{R} \right)\]
\[ \Rightarrow \left( \frac{a}{x} \right) = \left( \frac{g}{R} \right)\]
\[\Rightarrow a = x\frac{g}{R}\]
As acceleration is directly proportional to the displacement. Hence, the body will execute S.H.M.
Time period \[\left( T \right)\] is given by,
\[T = 2\pi\sqrt{\frac{\text { displacement }}{\text { Acceleration }}}\]
\[= 2\pi\sqrt{\frac{x}{gx/R}} = 2\pi\sqrt{\frac{R}{g}}\]
APPEARS IN
RELATED QUESTIONS
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses Pand Q equal number of times in a given time interval. Does it make you unhappy?
Can a pendulum clock be used in an earth-satellite?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
The average energy in one time period in simple harmonic motion is
A pendulum clock keeping correct time is taken to high altitudes,
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
Which of the following quantities are always positive in a simple harmonic motion?
A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
A particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45° with the X-axis. The two motions are given by x = x0 sin ωt and s = s0 sin ωt. Find the amplitude of the resultant motion.
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
Define the frequency of simple harmonic motion.
What is meant by simple harmonic oscillation? Give examples and explain why every simple harmonic motion is a periodic motion whereas the converse need not be true.
A simple harmonic motion is given by, x = 2.4 sin ( 4πt). If distances are expressed in cm and time in seconds, the amplitude and frequency of S.H.M. are respectively,
The displacement of a particle is represented by the equation y = sin3ωt. The motion is ______.
If x = `5 sin (pi t + pi/3) m` represents the motion of a particle executing simple harmonic motion, the amplitude and time period of motion, respectively, are ______.
