Advertisements
Advertisements
Question
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
Solution
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
In S.H.M.,
F = -kx
Therefore,
\[\vec{F} . \vec{r} .\] will always be negative. As acceleration has the same direction as the force,
\[\vec{a} . \vec{r} \] Will also be negative , always .
APPEARS IN
RELATED QUESTIONS
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on a horizontal plane move in a sample harmonic motion?
Can a pendulum clock be used in an earth-satellite?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
A particle moves in a circular path with a continuously increasing speed. Its motion is
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
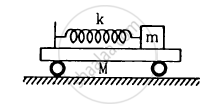
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
