Advertisements
Advertisements
Question
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
Solution
Given: T = 10 s
P. E = `1/2 (T.E)`
To find: Time (t)

∴ t = 1.25 s
The time in which the potential energy will be half of total energy is 1.25 s.
APPEARS IN
RELATED QUESTIONS
A particle in S.H.M. has a period of 2 seconds and amplitude of 10 cm. Calculate the acceleration when it is at 4 cm from its positive extreme position.
The average displacement over a period of S.H.M. is ______.
(A = amplitude of S.H.M.)
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate:
a) Angular frequency
b) frequency of vibration.
State the differential equation of linear simple harmonic motion.
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The displacement of a particle in simple harmonic motion in one time period is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
A pendulum clock keeping correct time is taken to high altitudes,
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
Which of the following quantities are always positive in a simple harmonic motion?
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
Which of the following will change the time period as they are taken to moon?
(a) A simple pendulum
(b) A physical pendulum
(c) A torsional pendulum
(d) A spring-mass system
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.
What is an epoch?
Write short notes on two springs connected in parallel.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
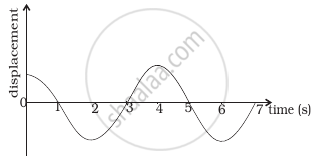
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
The velocities of a particle in SHM at positions x1 and x2 are v1 and v2 respectively, its time period will be ______.
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
