Advertisements
Advertisements
Question
Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.
Solution
It is given that three S.H.M.s of equal amplitudes A and equal time periods are combined in the same direction.
Let
\[Y_1 , Y_2 \text { and } Y_3\] be the three vectors representing the motions, as shown in the figure given below.
According to the question:
\[\text { Angle between } Y_1 \text { and } Y_2 = 60 ^\circ\]
\[\text { Angle between } Y_2 \text{ and } Y_3 = 60 ^\circ\]
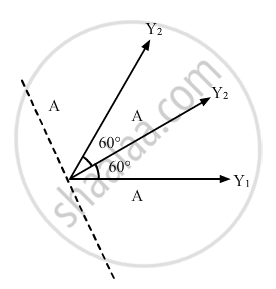
By using the vector method, we can find the resultant vector.
Resultant amplitude = Vector sum of the three vectors
= A + A cos 60° + A cos 60°
\[= A + \frac{A}{2} + \frac{A}{2} = 2A\]
APPEARS IN
RELATED QUESTIONS
Define phase of S.H.M.
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
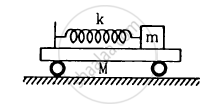
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π/3 seconds to complete one oscillation. Find the acceleration of the elevator.
What is an epoch?
Write short notes on two springs connected in series.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
A simple harmonic motion is given by, x = 2.4 sin ( 4πt). If distances are expressed in cm and time in seconds, the amplitude and frequency of S.H.M. are respectively,
What is the ratio of maxmimum acceleration to the maximum velocity of a simple harmonic oscillator?
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
