Advertisements
Advertisements
Question
A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π/3 seconds to complete one oscillation. Find the acceleration of the elevator.
Solution
It is given that:
Length of the simple pendulum, l = 1 feet
Time period of simple pendulum, T = \[\frac{\pi}{3} s\] Acceleration due to gravity, g = 32 ft/s2
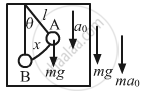
Let a be the acceleration of the elevator while moving upwards.
Driving force \[\left( f \right)\] is given by,
f = m(g + a)sinθ
Comparing the above equation with the expression, f = ma, we get:
Acceleration, a = (g + a)sinθ = (g +a)θ (For small angle θ, sin θ → θ)
\[= \frac{\left( g + a \right)x}{l} = \omega^2 x\] (From the diagram \[\theta = \frac{x}{l}\])
\[\Rightarrow \omega = \sqrt{\frac{\left( g + a \right)}{l}}\]
Time Period \[\left( T \right)\] is given as,
\[T = 2\pi\sqrt{\frac{l}{g + a}}\]
On substituting the respective values in the above formula, we get:
\[\frac{\pi}{3} = 2\pi\sqrt{\frac{1}{32 + a}}\]
\[\frac{1}{9} = 4\left( \frac{1}{32 + a} \right)\]
\[ \Rightarrow 32 + a = 36\]
\[ \Rightarrow a = 36 - 32 = 4 ft/ s^2\]
APPEARS IN
RELATED QUESTIONS
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses Pand Q equal number of times in a given time interval. Does it make you unhappy?
A pendulum clock gives correct time at the equator. Will it gain time or loose time as it is taken to the poles?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
A pendulum clock keeping correct time is taken to high altitudes,
A pendulum clock keeping correct time is taken to high altitudes,
Which of the following quantities are always positive in a simple harmonic motion?
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
In a simple harmonic motion
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
A simple pendulum fixed in a car has a time period of 4 seconds when the car is moving uniformly on a horizontal road. When the accelerator is pressed, the time period changes to 3.99 seconds. Making an approximate analysis, find the acceleration of the car.
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
Describe Simple Harmonic Motion as a projection of uniform circular motion.
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______.
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
