Advertisements
Advertisements
Question
In a simple harmonic motion
Options
the potential energy is always equal to the kinetic energy
the potential energy is never equal to the kinetic energy
the average potential energy in any time interval is equal to the average kinetic energy in that time interval
the average potential energy in one time period is equal to the average kinetic energy in this period.
Solution
the average potential energy in one time period is equal to the average kinetic energy in this period.
The kinetic energy of the motion is given as,
\[\frac{1}{2}k A^2 \cos^2 \omega t\]
The potential energy is calculated as,
APPEARS IN
RELATED QUESTIONS
In a damped harmonic oscillator, periodic oscillations have _______ amplitude.
(A) gradually increasing
(B) suddenly increasing
(C) suddenly decreasing
(D) gradually decreasing
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
The energy of system in simple harmonic motion is given by \[E = \frac{1}{2}m \omega^2 A^2 .\] Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
A particle moves in the X-Y plane according to the equation \[\overrightarrow{r} = \left( \overrightarrow{i} + 2 \overrightarrow{j} \right)A\cos\omega t .\]
The motion of the particle is
(a) on a straight line
(b) on an ellipse
(c) periodic
(d) simple harmonic
A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
Define the time period of simple harmonic motion.
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
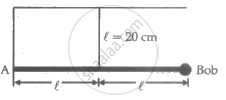
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
