Advertisements
Advertisements
Question
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
Solution
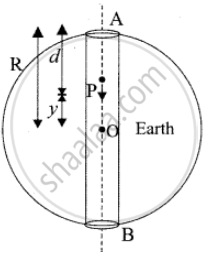
Oscillations of a particle dropped in a tunnel along the diameter of the earth.
Consider earth to be a sphere of radius R and centre O. A straight tunnel is dug along the diameter of the earth. Let ‘g’ be the value of acceleration due to gravity at the surface of the earth.
Suppose a body of mass ‘m’ is dropped into the tunnel and it is at point R i.e., at a depth d below the surface of the earth at any instant.
If g’ is the acceleration due to gravity at P.
then R − d = y
∴ g’ = `"g"("y"/"R")`
Force acting on the body a point P is
F = − mg’ = `-"mg"/"R""y"` i.e., `"F" ∝ "y"`
Negative sign indicates that the force acts in the opposite direction of displacement.
Thus the body will execute SHM with force constant, k = `"mg"/"R"`
The period of oscillation of the body will be T = `2π sqrt("m"/"k") = 2π sqrt ("m"/("mg"//"R"))`
T = `2π sqrt("R"/"g")`
APPEARS IN
RELATED QUESTIONS
State the differential equation of linear simple harmonic motion.
A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses Pand Q equal number of times in a given time interval. Does it make you unhappy?
Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?
The average energy in one time period in simple harmonic motion is
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
A body having specific charge 8 µC/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally toward the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be ______ s.

