Question

A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?

Answer 1

\[\frac{18}{100} = 0 . 18  m = 0 . 2  m\]

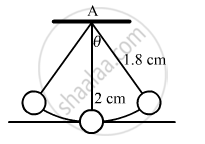
Let I be the moment of inertia and \[\omega\] be the angular speed.
Using the energy equation, we can write:

\[mgl(1 - \cos  \theta) + \frac{1}{2}I \omega^2  = \text { constant }\]

\[mg\left( 0 . 20 \right)  \left( 1 - \cos  \theta \right) + \frac{1}{2}I \omega^2  = C                           .  .  . \left( 1 \right)\] 

\[\text { Moment  of  inertia  about  the  point  of  suspension  A  is  given  by, } \] 

\[I = \frac{2}{3}m r^2  + m l^2 \] 

\[\text { Substituting  the  value  of  l  in  the  above  equation,   we  get: }\] 

\[I = \frac{2}{3}m \left( 0 . 02 \right)^2  + m   \left( 0 . 2 \right)^2 \] 

\[   = \frac{2}{3}m\left( 0 . 0004 \right) + m\left( 0 . 04 \right)\] 

\[   = m\left[ \frac{0 . 0008}{3} + 0 . 04 \right]\] 

\[   = m\left( \frac{0 . 1208}{3} \right)\]

On substituting the value of I in equation (1) and differentiating it, we get:

\[\frac{d}{dt}\left[ mg  \left( 0 . 2 \right)  \left( 1 - \cos  \theta \right) + \frac{1}{2}\frac{0 . 1208}{3}m \omega^2 \right] = \frac{d}{dt}\left( c \right)\] 

\[ \Rightarrow mg\left( 0 . 2 \right)\sin\theta\frac{d\theta}{dt} + \frac{1}{2}\left( \frac{0 . 1208}{3} \right)m \times 2\omega\frac{d\omega}{dt} = 0  \] 

\[ \Rightarrow 2\sin  \theta = \frac{0 . 1208}{3}\alpha                          \left[ \text { because }, g = 10  m/ s^2 \right]\] 

\[ \Rightarrow \frac{\alpha}{\theta} = \frac{6}{0 . 1208}\] 

\[ \Rightarrow  \omega^2  = 49 . 66\] 

\[ \Rightarrow \omega = 7 . 04\] 

\[\text { Thus,   time  period }\left( T \right) \text { will  be: }\] 

\[T = \frac{2\pi}{\omega} = 0 . 89  s\]

For a simple pendulum, time period (T) is given by,

\[T = 2\pi\sqrt{\frac{l}{g}}\]

\[\Rightarrow T =   2\pi\sqrt{\frac{0 . 18}{10}}\] = 0.86 s
%   change  in  the  value  of  time  period = \[\frac{0 . 89 - 0 . 86}{0 . 89} \times 100 = 0 . 3\]

∴ It is about 0.3% greater than the calculated value.