Advertisements
Advertisements
Question
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s2?
Advertisements
Solution
It is given that:
Length of the pendulum, l = 5 m
Acceleration due to gravity, g = 9.8 ms-2
Acceleration due to gravity at the moon, g' = 1.67 ms-2
(a) Time period \[\left( T \right)\] is given by,
\[T = 2\pi\sqrt{\frac{l}{g}}\]
\[= 2\pi\sqrt{\frac{5}{9 . 8}}\]
\[ = 2\pi\sqrt{0 . 510} = 2\pi \left( 0 . 71 \right) s\]
i.e. the body will take 2 \[\pi\](0.7) seconds to complete an oscillation.
Now, frequency \[\left( f \right)\]is given by,
\[f = \frac{1}{T}\]
\[\therefore f = \frac{1}{2\pi\left( 0 . 71 \right)} \]
\[ = \frac{0 . 70}{\pi} Hz\]
(b) Let
\[g'\] be the value of acceleration due to gravity at moon. Time period of simple pendulum at moon \[\left( T' \right)\],is given as:
\[T' = 2\pi\sqrt{\left( \frac{l}{g'} \right)}\]
On substituting the respective values in the above formula, we get:
\[ = \frac{1}{2\pi}\sqrt{\frac{1 . 67}{5}} = \frac{1}{2\pi}\left( 0 . 577 \right)\]
\[ = \frac{1}{2\pi\sqrt{3}} Hz\]
APPEARS IN
RELATED QUESTIONS
Define phase of S.H.M.
State the differential equation of linear simple harmonic motion.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
A pendulum clock gives correct time at the equator. Will it gain time or loose time as it is taken to the poles?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The displacement of a particle in simple harmonic motion in one time period is
A pendulum clock keeping correct time is taken to high altitudes,
The motion of a torsional pendulum is
(a) periodic
(b) oscillatory
(c) simple harmonic
(d) angular simple harmonic
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
Write short notes on two springs connected in parallel.
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______
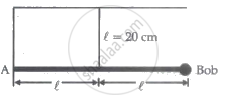
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)
If x = `5 sin (pi t + pi/3) m` represents the motion of a particle executing simple harmonic motion, the amplitude and time period of motion, respectively, are ______.
