Advertisements
Advertisements
Question
A small block oscillates back and forth on a smooth concave surface of radius R ib Figure . Find the time period of small oscillation.
Advertisements
Solution
The maximum tension in the string of an oscillating pendulum is double of the minimum tension. Find the angular amplitude.
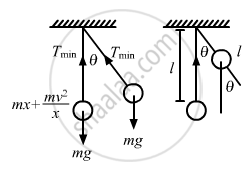
Let the speed of bob of the pendulum at an angle \[\theta\] be v.
Using the principle of conservation of energy between the mean and extreme positions, we get:
\[\frac{1}{2}\]mv2 − 0 = mgl(1 − cos θ)
v2 = 2gl(1 − cos θ) ...(1)
In a moving pendulum, the tension is maximum at the mean position, whereas it is minimum at the extreme position.
Maximum tension at the mean position is given by
Tmax = mg + 2mg(1 − cos θ)
Minimum tension at the extreme position is given by
Tmin = m g cosθ
According to the question,
Tmax = 2Tmin
⇒ mg + 2mg − 2m g cosθ = 2m g cosθ
⇒ 3mg = 4 mg cosθ
\[\Rightarrow \cos \theta = \frac{3}{4}\]
\[ \Rightarrow \theta = \cos^{- 1} \frac{3}{4}\]
APPEARS IN
RELATED QUESTIONS
Define phase of S.H.M.
In a damped harmonic oscillator, periodic oscillations have _______ amplitude.
(A) gradually increasing
(B) suddenly increasing
(C) suddenly decreasing
(D) gradually decreasing
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate:
a) Angular frequency
b) frequency of vibration.
A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on a horizontal plane move in a sample harmonic motion?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
A particle moves in the X-Y plane according to the equation \[\overrightarrow{r} = \left( \overrightarrow{i} + 2 \overrightarrow{j} \right)A\cos\omega t .\]
The motion of the particle is
(a) on a straight line
(b) on an ellipse
(c) periodic
(d) simple harmonic
In a simple harmonic motion
(a) the maximum potential energy equals the maximum kinetic energy
(b) the minimum potential energy equals the minimum kinetic energy
(c) the minimum potential energy equals the maximum kinetic energy
(d) the maximum potential energy equals the minimum kinetic energy
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A particle executing SHM crosses points A and B with the same velocity. Having taken 3 s in passing from A to B, it returns to B after another 3 s. The time period is ____________.
Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
The displacement of a particle is represented by the equation y = sin3ωt. The motion is ______.
The displacement of a particle varies with time according to the relation y = a sin ωt + b cos ωt.
Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is ______.
- simple harmonic motion.
- non-periodic motion.
- periodic motion.
- periodic but not S.H.M.
If x = `5 sin (pi t + pi/3) m` represents the motion of a particle executing simple harmonic motion, the amplitude and time period of motion, respectively, are ______.
