Advertisements
Advertisements
प्रश्न
A small block oscillates back and forth on a smooth concave surface of radius R ib Figure . Find the time period of small oscillation.
उत्तर
The maximum tension in the string of an oscillating pendulum is double of the minimum tension. Find the angular amplitude.
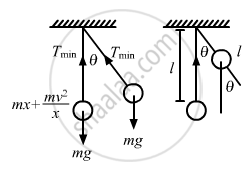
Let the speed of bob of the pendulum at an angle \[\theta\] be v.
Using the principle of conservation of energy between the mean and extreme positions, we get:
\[\frac{1}{2}\]mv2 − 0 = mgl(1 − cos θ)
v2 = 2gl(1 − cos θ) ...(1)
In a moving pendulum, the tension is maximum at the mean position, whereas it is minimum at the extreme position.
Maximum tension at the mean position is given by
Tmax = mg + 2mg(1 − cos θ)
Minimum tension at the extreme position is given by
Tmin = m g cosθ
According to the question,
Tmax = 2Tmin
⇒ mg + 2mg − 2m g cosθ = 2m g cosθ
⇒ 3mg = 4 mg cosθ
\[\Rightarrow \cos \theta = \frac{3}{4}\]
\[ \Rightarrow \theta = \cos^{- 1} \frac{3}{4}\]
APPEARS IN
संबंधित प्रश्न
A particle in S.H.M. has a period of 2 seconds and amplitude of 10 cm. Calculate the acceleration when it is at 4 cm from its positive extreme position.
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x
(b) a = –200x2
(c) a = –10x
(d) a = 100x3
In a damped harmonic oscillator, periodic oscillations have _______ amplitude.
(A) gradually increasing
(B) suddenly increasing
(C) suddenly decreasing
(D) gradually decreasing
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
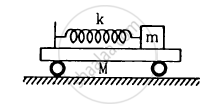
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s2?
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
Define the time period of simple harmonic motion.
What is meant by simple harmonic oscillation? Give examples and explain why every simple harmonic motion is a periodic motion whereas the converse need not be true.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
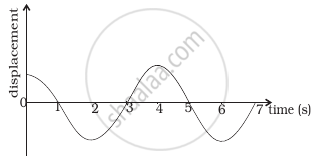
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
