Question

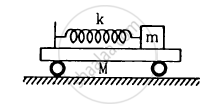
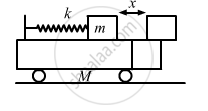
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x₀ when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.

Answer 1

Let x₁ and x₂ be the amplitudes of oscillation of masses m and M respectively.

(a) As the centre of mass should not change during the motion, we can write:
           mx₁ = Mx₂                \[\ldots(1)\]

Let k be the spring constant. By conservation of energy, we have:

\[\frac{1}{2}k x_0^2  = \frac{1}{2}k \left( x_1 + x_2 \right)^2                                       \ldots(2)\]

     where x₀ is the length to which spring is stretched.

From equation (2) we have,

\[x_0  =  x_1  +  x_2 \]

On substituting the value of x₂ from equation (1) in equation (2), we get:

\[x_0  =  x_1  + \frac{m x_1}{M}\] 

\[ \Rightarrow  x_0  = \left( 1 + \frac{m}{M} \right) x_1 \] 

\[ \Rightarrow  x_1  = \left( \frac{M}{M + m} \right) x_0\]

\[\text { Now },    x_2  =  x_0  -  x_1 \] 

On substituting the value of x₁ from above equation, we get:    

\[\Rightarrow    x_2  =  x_0 \left[ 1 - \frac{M}{M + m} \right]\] 

\[ \Rightarrow    x_2  = \frac{m x_0}{M + m}\]

Thus, the amplitude of the simple harmonic motion of a car, as seen from the road is

\[\frac{m x_0}{M + m}\]

(b) At any position,
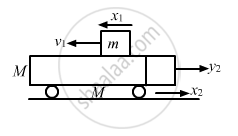
Let v₁ and v₂ be the velocities.

Using law of conservation of energy we have,

\[\frac{1}{2}M v^2  + \frac{1}{2}m \left( v_1 - v_2 \right)^2  + \frac{1}{2}k \left( x_1 + x_2 \right)^2  = \text { constant }                                 .  .  . \left( 3 \right)\]

Here, (v₁ − v₂) is the absolute velocity of mass m as seen from the road.

Now, from the principle of conservation of momentum, we have:
Mx₂ = mx₁

\[\Rightarrow  x_1  = \left( \frac{M}{m} \right) x_2                                  .  .  .  . \left( 4 \right)\] 

\[M v_2  = m\left( v_1 - v_2 \right)\] 

\[ \Rightarrow \left( v_1 - v_2 \right) = \left( \frac{M}{m} \right) v_2              .  .  .  . \left( 5 \right)\]

Putting the above values in equation (3), we get:

\[\frac{1}{2}M v_2^2  + \frac{1}{2}m\frac{M^2}{m^2} v_2^2  + \frac{1}{2}k x_2^2  \left( 1 + \frac{M}{m} \right)^2  = \text { constant }\] 

\[ \therefore M\left( 1 + \frac{M}{m} \right) v_2^2  + k\left( 1 + \frac{M}{m} \right) x_2^2  = \text { constant } \] 

\[ \Rightarrow M v_2^2  + k\left( 1 + \frac{M}{m} \right) x_2^2  = \text { constant } \]

Taking derivative of both the sides, we get:

\[M \times 2 v_2 \frac{d v_2}{dt} + k\left( \frac{M + m}{m} \right)2 x_2 \frac{d x_2}{dt} = 0\] 

\[ \Rightarrow m a_2  + k\left( \frac{M + m}{m} \right) x_2  = 0                        \left[ \text { because }, v_2 = \frac{d x_2}{dt} \right]\] 

\[\frac{a_2}{x_2} = \frac{- k\left( M + m \right)}{Mm} =  \omega^2 \] 

\[ \therefore \omega = \sqrt{\frac{k\left( M + m \right)}{Mm}}\] 

\[\text { Therefore,   time  period },   T = 2\pi\sqrt{\frac{Mm}{k\left( M + m \right)}}\]