Advertisements
Advertisements
प्रश्न
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
उत्तर
Displacement-time graph:
i.
At extreme position, α = π/2
Displacement, x = A cos ωt
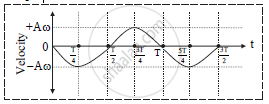
Velocity time graph:
i.
At extreme position, α = π/2
Velocity of a particle is v = - Aω sin ωt
ii. Table:
Substituting ω = 2π/T in above equation,
| Time (t) | Phase (ωt) | Velocity (v) |
| 0 | 0 | 0 |
| T/4 | π/2 | -Aω |
| T/2 | π | 0 |
| 3T/4 | 3π/2 | Aω |
| T | 2π | 0 |
Graph:
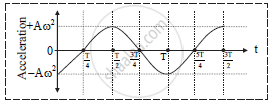
Acceleration-time graph:
i. At extreme position,α = π/2
Acceleration of a particle is,
a =-Aω2 cos ωt
ii. Table:
Substituting ω = 2π/T in above equation
| Time (t) | Phase (ωt) | Velocity (v) |
| 0 | 0 | -Aω2 |
| T/4 | π/2 | 0 |
| T/2 | π | Aω2 |
| 3T/4 | 3π/2 | 0 |
| T | 2π | -Aω2 |
iii. Graph:
Conclusions:
i. Displacement, velocity and acceleration of S.H.M. are periodic functions of time.
ii. The displacement and acceleration curves are sine curves whereas velocity curve is
cosine curve (α = 0).
iii. The phase difference between displacement and acceleration is of π radian.
iv. The phase difference between displacement and velocity and velocity and acceleration
is of π/2 radian.
v. The displacement and acceleration is maximum at extreme position whereas velocity is
minimum at the same position.
vi. All curves repeat same path after phase of 2π radian.
APPEARS IN
संबंधित प्रश्न
In a damped harmonic oscillator, periodic oscillations have _______ amplitude.
(A) gradually increasing
(B) suddenly increasing
(C) suddenly decreasing
(D) gradually decreasing
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate:
a) Angular frequency
b) frequency of vibration.
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
The energy of system in simple harmonic motion is given by \[E = \frac{1}{2}m \omega^2 A^2 .\] Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
A pendulum clock gives correct time at the equator. Will it gain time or loose time as it is taken to the poles?
Can a pendulum clock be used in an earth-satellite?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
For a particle executing simple harmonic motion, the acceleration is proportional to
A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.
The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on the surface of planet X such that the acceleration of the planet X is n times greater than the Earth is
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
State the laws of the simple pendulum?
A simple harmonic motion is given by, x = 2.4 sin ( 4πt). If distances are expressed in cm and time in seconds, the amplitude and frequency of S.H.M. are respectively,
A body having specific charge 8 µC/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally toward the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be ______ s.

A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.

Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
