Advertisements
Advertisements
Question
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
Solution
Displacement-time graph:
i.
At extreme position, α = π/2
Displacement, x = A cos ωt
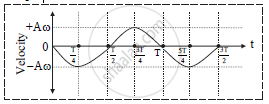
Velocity time graph:
i.
At extreme position, α = π/2
Velocity of a particle is v = - Aω sin ωt
ii. Table:
Substituting ω = 2π/T in above equation,
| Time (t) | Phase (ωt) | Velocity (v) |
| 0 | 0 | 0 |
| T/4 | π/2 | -Aω |
| T/2 | π | 0 |
| 3T/4 | 3π/2 | Aω |
| T | 2π | 0 |
Graph:
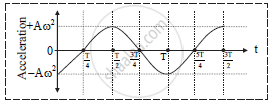
Acceleration-time graph:
i. At extreme position,α = π/2
Acceleration of a particle is,
a =-Aω2 cos ωt
ii. Table:
Substituting ω = 2π/T in above equation
| Time (t) | Phase (ωt) | Velocity (v) |
| 0 | 0 | -Aω2 |
| T/4 | π/2 | 0 |
| T/2 | π | Aω2 |
| 3T/4 | 3π/2 | 0 |
| T | 2π | -Aω2 |
iii. Graph:
Conclusions:
i. Displacement, velocity and acceleration of S.H.M. are periodic functions of time.
ii. The displacement and acceleration curves are sine curves whereas velocity curve is
cosine curve (α = 0).
iii. The phase difference between displacement and acceleration is of π radian.
iv. The phase difference between displacement and velocity and velocity and acceleration
is of π/2 radian.
v. The displacement and acceleration is maximum at extreme position whereas velocity is
minimum at the same position.
vi. All curves repeat same path after phase of 2π radian.
APPEARS IN
RELATED QUESTIONS
A particle in S.H.M. has a period of 2 seconds and amplitude of 10 cm. Calculate the acceleration when it is at 4 cm from its positive extreme position.
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
A pendulum clock keeping correct time is taken to high altitudes,
A particle moves in a circular path with a continuously increasing speed. Its motion is
Which of the following quantities are always zero in a simple harmonic motion?
(a) \[\vec{F} \times \vec{a} .\]
(b) \[\vec{v} \times \vec{r} .\]
(c) \[\vec{a} \times \vec{r} .\]
(d) \[\vec{F} \times \vec{r} .\]
For a particle executing simple harmonic motion, the acceleration is proportional to
An object is released from rest. The time it takes to fall through a distance h and the speed of the object as it falls through this distance are measured with a pendulum clock. The entire apparatus is taken on the moon and the experiment is repeated
(a) the measured times are same
(b) the measured speeds are same
(c) the actual times in the fall are equal
(d) the actual speeds are equal
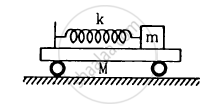
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A small block oscillates back and forth on a smooth concave surface of radius R ib Figure . Find the time period of small oscillation.
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
Define the time period of simple harmonic motion.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
The displacement of a particle is represented by the equation `y = 3 cos (pi/4 - 2ωt)`. The motion of the particle is ______.
