Advertisements
Advertisements
Question
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
Solution
It is given that a particle is subjected to two S.H.M.s of same time period in the same direction.
Amplitude of first motion, A1 = 3 cm
Amplitude of second motion, A2 = 4 cm
Let ϕ be the phase difference.
The resultant amplitude \[\left( R \right)\] is given by,
\[R = \sqrt{A_1^2 + A_2^2 + 2 A_1 A_2 cos \phi}\]
(a) When ϕ = 0°
\[R = \sqrt{\left( 3^2 + 4^2 + \left( 2 \right)\left( 3 \right)\left( 4 \right) \cos 0^\circ\right)}\]
\[ = 7 \text { cm }\]
(b) When ϕ = 60°
\[R = \sqrt{3^2 + 4^2 + \left( 2 \right)\left( 3 \right)\left( 4 \right) \cos 60^\circ}\]
\[ = \sqrt{37} = 6 . 1 \text { cm }\]
(c) When ϕ = 90°
\[R = \sqrt{\left( 3^2 + 4^2 + \left( 2 \right)\left( 3 \right)\left( 4 \right)\cos 90^\circ\right)}\]
\[ = \sqrt{25} = 5 \text { cm }\]
APPEARS IN
RELATED QUESTIONS
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
Figure represents two simple harmonic motions.
The parameter which has different values in the two motions is

A particle moves in the X-Y plane according to the equation \[\overrightarrow{r} = \left( \overrightarrow{i} + 2 \overrightarrow{j} \right)A\cos\omega t .\]
The motion of the particle is
(a) on a straight line
(b) on an ellipse
(c) periodic
(d) simple harmonic
A small block oscillates back and forth on a smooth concave surface of radius R ib Figure . Find the time period of small oscillation.
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be __________.
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
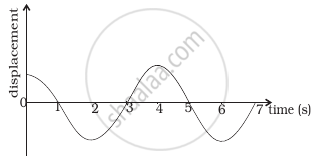
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
A body having specific charge 8 µC/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally toward the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be ______ s.

The velocities of a particle in SHM at positions x1 and x2 are v1 and v2 respectively, its time period will be ______.
Assume there are two identical simple pendulum clocks. Clock - 1 is placed on the earth and Clock - 2 is placed on a space station located at a height h above the earth's surface. Clock - 1 and Clock - 2 operate at time periods 4 s and 6 s respectively. Then the value of h is ______.
(consider the radius of earth RE = 6400 km and g on earth 10 m/s2)
