Advertisements
Advertisements
प्रश्न
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
उत्तर
Displacement-time graph:
i.
At extreme position, α = π/2
Displacement, x = A cos ωt
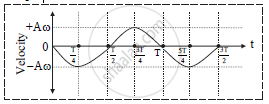
Velocity time graph:
i.
At extreme position, α = π/2
Velocity of a particle is v = - Aω sin ωt
ii. Table:
Substituting ω = 2π/T in above equation,
| Time (t) | Phase (ωt) | Velocity (v) |
| 0 | 0 | 0 |
| T/4 | π/2 | -Aω |
| T/2 | π | 0 |
| 3T/4 | 3π/2 | Aω |
| T | 2π | 0 |
Graph:
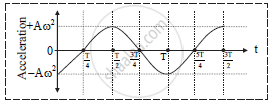
Acceleration-time graph:
i. At extreme position,α = π/2
Acceleration of a particle is,
a =-Aω2 cos ωt
ii. Table:
Substituting ω = 2π/T in above equation
| Time (t) | Phase (ωt) | Velocity (v) |
| 0 | 0 | -Aω2 |
| T/4 | π/2 | 0 |
| T/2 | π | Aω2 |
| 3T/4 | 3π/2 | 0 |
| T | 2π | -Aω2 |
iii. Graph:
Conclusions:
i. Displacement, velocity and acceleration of S.H.M. are periodic functions of time.
ii. The displacement and acceleration curves are sine curves whereas velocity curve is
cosine curve (α = 0).
iii. The phase difference between displacement and acceleration is of π radian.
iv. The phase difference between displacement and velocity and velocity and acceleration
is of π/2 radian.
v. The displacement and acceleration is maximum at extreme position whereas velocity is
minimum at the same position.
vi. All curves repeat same path after phase of 2π radian.
APPEARS IN
संबंधित प्रश्न
The average displacement over a period of S.H.M. is ______.
(A = amplitude of S.H.M.)
State the differential equation of linear simple harmonic motion.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
A particle executes simple harmonic motion. If you are told that its velocity at this instant is zero, can you say what is its displacement? If you are told that its velocity at this instant is maximum, can you say what is its displacement?
A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on a horizontal plane move in a sample harmonic motion?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
For a particle executing simple harmonic motion, the acceleration is proportional to
A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on the surface of planet X such that the acceleration of the planet X is n times greater than the Earth is
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
Define the frequency of simple harmonic motion.
What is an epoch?
Write short notes on two springs connected in parallel.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______.
The displacement of a particle varies with time according to the relation y = a sin ωt + b cos ωt.
The velocities of a particle in SHM at positions x1 and x2 are v1 and v2 respectively, its time period will be ______.
