Question

Assume that a tunnel is dug across the earth (radius = R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of \[\sqrt{gR}\] (b) it is released from a height R above the tunnel (c) it is thrown vertically upward along the length of tunnel with a speed of \[\sqrt{gR}\]

Answer 1

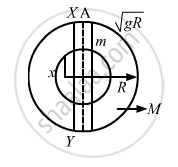
Given:
Radius of the earth is R.
Let M be the total mass of the earth and \[\rho\] be the density.
Let mass of the part of earth having radius x be M.

\[\therefore \frac{M'}{M} = \frac{\rho \times \frac{4}{3}\pi x^3}{\rho \times \frac{4}{3}\pi R^3} = \frac{x^3}{R^3}\] 

\[ \Rightarrow M' = \frac{M x^3}{R^3}\]

Force on the particle is calculated as,

\[F_x  = \frac{GM'm}{x^2}\] 

\[       = \frac{GMm}{R^3}x                          \ldots\left( 1 \right)\]

Now, acceleration \[\left( a_x \right)\] of mass M' at that position is given by,

\[a_x  = \frac{GM}{R^3}x\] 

\[ \Rightarrow \frac{a_x}{x} =  \omega^2  = \frac{GM}{R^3} = \frac{g}{R}                                \left( \because g = \frac{GM}{R^2} \right)\] 

\[\text{So,   Time  period  of  oscillation ,}   T = 2\pi\sqrt{\left( \frac{R}{g} \right)}\]

(a) Velocity-displacement equation in S.H.M is written as,

\[V = \omega\sqrt{\left( A^2 - y^2 \right)} \]      

where,   A  is  the  amplitude;   and                              y  is  the  displacement .

When the particle is at y = R,
The velocity of the particle is \[\sqrt{gR}\] and \[\omega = \sqrt{\frac{g}{R}}\]

On substituting these values in the velocity-displacement equation, we get:

\[\sqrt{gR} = \sqrt{\frac{g}{R}}\sqrt{A^2 - R^2}                    \] 

\[ \Rightarrow  R^2  =  A^2  -  R^2 \] 

\[ \Rightarrow A = \sqrt{2R}\]

Let t₁ and t₂ be the time taken by the particle to reach the positions X and Y.
Now, phase of the particle at point X will be greater than \[\frac{\pi}{2}\] but less than \[\pi\]

Also, the phase of the particle on reaching Y will be greater than \[\pi\] but less than \[\frac{3\pi}{2}\]

Displacement-time relation is given by,
y = A sin ωt

Substituting y = R and A =\[\sqrt{2R}\] , in the above relation , we get :

\[R = \sqrt{2}R  \sin  \omega t_1\]

\[\Rightarrow \omega t_1  = \frac{3\pi}{4}\]

Also,

\[R = \sqrt{2}R  \sin  \omega t_2\]

\[\Rightarrow \omega t_2  = \frac{5\pi}{4}\] 

\[\text{So},   \omega\left( t_2 - t_1 \right) = \frac{\pi}{2}\] 

\[ \Rightarrow  t_2  -  t_1  = \frac{\pi}{2\omega} = \frac{\pi}{2\left( \sqrt{\frac{g}{R}} \right)}\]

Time taken by the particle to travel from X to Y:

\[t_2  -  t_1  = \frac{\pi}{2\omega} = \frac{\pi}{2}\sqrt{\frac{R}{g}}\] s

(b) When the body is dropped from a height R

      Using the principle of conservation of energy, we get:
      Change in P.E. = Gain in K.E.

\[\Rightarrow \frac{GMm}{R} - \frac{GMm}{2R} = \frac{1}{2}m v^2 \] 

\[ \Rightarrow v = \sqrt{\left( gR \right)}\]

As the velocity is same as that at X, the body will take the same time to travel XY.

(c) The body is projected vertically upwards from the point X with a velocity \[\sqrt{gR}\].Its velocity becomes zero as it reaches the highest point.
      The velocity of the body as it reaches X again will be,

\[v = \sqrt{\left( gR \right)}\]

    Hence, the body will take same time i.e.

\[\frac{\pi}{2}\sqrt{\left( \frac{R}{g} \right)}\]s to travel XY.