Advertisements
Advertisements
प्रश्न
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.

उत्तर
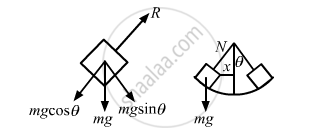
It is given that R is the radius of the concave surface.
Let N be the normal reaction force.
Driving force, F = mg sin θ
Comparing the expression for driving force with the expression, F = ma, we get:
Acceleration, a = g sin θ
Since the value of θ is very small,
∴ sin θ → θ
∴ Acceleration, a = gθ
Let x be the displacement of the body from mean position.
\[\therefore \theta = \frac{x}{R}\]
\[ \Rightarrow a = g\theta = g\left( \frac{x}{R} \right)\]
\[ \Rightarrow \left( \frac{a}{x} \right) = \left( \frac{g}{R} \right)\]
\[\Rightarrow a = x\frac{g}{R}\]
As acceleration is directly proportional to the displacement. Hence, the body will execute S.H.M.
Time period \[\left( T \right)\] is given by,
\[T = 2\pi\sqrt{\frac{\text { displacement }}{\text { Acceleration }}}\]
\[= 2\pi\sqrt{\frac{x}{gx/R}} = 2\pi\sqrt{\frac{R}{g}}\]
APPEARS IN
संबंधित प्रश्न
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x
(b) a = –200x2
(c) a = –10x
(d) a = 100x3
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
In measuring time period of a pendulum, it is advised to measure the time between consecutive passage through the mean position in the same direction. This is said to result in better accuracy than measuring time between consecutive passage through an extreme position. Explain.
Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?
A block of known mass is suspended from a fixed support through a light spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
In a simple harmonic motion
(a) the maximum potential energy equals the maximum kinetic energy
(b) the minimum potential energy equals the minimum kinetic energy
(c) the minimum potential energy equals the maximum kinetic energy
(d) the maximum potential energy equals the minimum kinetic energy
An object is released from rest. The time it takes to fall through a distance h and the speed of the object as it falls through this distance are measured with a pendulum clock. The entire apparatus is taken on the moon and the experiment is repeated
(a) the measured times are same
(b) the measured speeds are same
(c) the actual times in the fall are equal
(d) the actual speeds are equal
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______
