Advertisements
Advertisements
प्रश्न
In a simple harmonic motion
(a) the maximum potential energy equals the maximum kinetic energy
(b) the minimum potential energy equals the minimum kinetic energy
(c) the minimum potential energy equals the maximum kinetic energy
(d) the maximum potential energy equals the minimum kinetic energy
उत्तर
(a) the maximum potential energy equals the maximum kinetic energy
(b) the minimum potential energy equals the minimum kinetic energy
In SHM,
maximum kinetic energy = \[\frac{1}{2}k A^2\]
maximum potential energy =\[\frac{1}{2}k A^2\]
The minimum value of both kinetic and potential energy is zero.
Therefore, in a simple harmonic motion the maximum kinetic energy and maximum potential energy are equal. Also, the minimum kinetic energy and the minimum potential energy are equal.
APPEARS IN
संबंधित प्रश्न
It is proposed to move a particle in simple harmonic motion on a rough horizontal surface by applying an external force along the line of motion. Sketch the graph of the applied force against the position of the particle. Note that the applied force has two values for a given position depending on whether the particle is moving in positive or negative direction.
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The average energy in one time period in simple harmonic motion is
A particle moves in a circular path with a continuously increasing speed. Its motion is
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
Which of the following quantities are always positive in a simple harmonic motion?
An object is released from rest. The time it takes to fall through a distance h and the speed of the object as it falls through this distance are measured with a pendulum clock. The entire apparatus is taken on the moon and the experiment is repeated
(a) the measured times are same
(b) the measured speeds are same
(c) the actual times in the fall are equal
(d) the actual speeds are equal
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s2?
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A simple pendulum fixed in a car has a time period of 4 seconds when the car is moving uniformly on a horizontal road. When the accelerator is pressed, the time period changes to 3.99 seconds. Making an approximate analysis, find the acceleration of the car.
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A simple pendulum has a time period T1. When its point of suspension is moved vertically upwards according to as y = kt2, where y is the vertical distance covered and k = 1 ms−2, its time period becomes T2. Then, T `"T"_1^2/"T"_2^2` is (g = 10 ms−2)
What is an epoch?
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
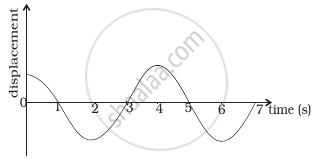
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
What is the ratio of maxmimum acceleration to the maximum velocity of a simple harmonic oscillator?
