Advertisements
Advertisements
Question
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
Solution
Given are the equations of motion of a particle:
x1 = 2.0sin100 \[\pi\]t
\[x_2 = 2 . 0\sin\left( 120\pi t + \frac{\pi}{3} \right)\]
The Resultant displacement \[\left( x \right)\] will be
x = x1 + x2
\[= 2\left[ \sin\left( 100\pi t \right) + \sin\left( 120\pi t + \frac{\pi}{3} \right) \right]\]
(a) At t = 0.0125 s
\[x = 2\left[ \sin\left( 100\pi \times 0 . 0125 \right) + \sin\left( 120\pi \times 0 . 0125 + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ \sin \left( \frac{5\pi}{4} \right) + \sin \left( \frac{3\pi}{2} + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ \left( - 0 . 707 \right) + \left( - 0 . 5 \right) \right]\]
\[ = 2 \times \left( - 1 . 207 \right) = - 2 . 41 cm\]
(b) At t = 0.025 s
\[x = 2\left[ \sin\left( 100 \pi \times 0 . 025 \right) + \sin\left( 120\pi \times 0 . 025 + \frac{\pi}{3} \right) \right]\] \[ = 2\left[ \sin\left( \frac{10\pi}{4} \right) + \sin\left( 3\pi + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ 1 + \left( - 0 . 866 \right) \right]\]
\[ = 2 \times \left( 0 . 134 \right) = 0 . 27 \text { cm }\]
APPEARS IN
RELATED QUESTIONS
Define phase of S.H.M.
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
A platoon of soldiers marches on a road in steps according to the sound of a marching band. The band is stopped and the soldiers are ordered to break the steps while crossing a bridge. Why?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The distance moved by a particle in simple harmonic motion in one time period is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
The average energy in one time period in simple harmonic motion is
A pendulum clock keeping correct time is taken to high altitudes,
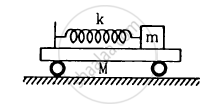
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
Define the frequency of simple harmonic motion.
Write short notes on two springs connected in series.
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______.
The displacement of a particle is represented by the equation `y = 3 cos (pi/4 - 2ωt)`. The motion of the particle is ______.
Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is ______.
- simple harmonic motion.
- non-periodic motion.
- periodic motion.
- periodic but not S.H.M.
