Advertisements
Advertisements
प्रश्न
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
उत्तर
Given are the equations of motion of a particle:
x1 = 2.0sin100 \[\pi\]t
\[x_2 = 2 . 0\sin\left( 120\pi t + \frac{\pi}{3} \right)\]
The Resultant displacement \[\left( x \right)\] will be
x = x1 + x2
\[= 2\left[ \sin\left( 100\pi t \right) + \sin\left( 120\pi t + \frac{\pi}{3} \right) \right]\]
(a) At t = 0.0125 s
\[x = 2\left[ \sin\left( 100\pi \times 0 . 0125 \right) + \sin\left( 120\pi \times 0 . 0125 + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ \sin \left( \frac{5\pi}{4} \right) + \sin \left( \frac{3\pi}{2} + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ \left( - 0 . 707 \right) + \left( - 0 . 5 \right) \right]\]
\[ = 2 \times \left( - 1 . 207 \right) = - 2 . 41 cm\]
(b) At t = 0.025 s
\[x = 2\left[ \sin\left( 100 \pi \times 0 . 025 \right) + \sin\left( 120\pi \times 0 . 025 + \frac{\pi}{3} \right) \right]\] \[ = 2\left[ \sin\left( \frac{10\pi}{4} \right) + \sin\left( 3\pi + \frac{\pi}{3} \right) \right]\]
\[ = 2\left[ 1 + \left( - 0 . 866 \right) \right]\]
\[ = 2 \times \left( 0 . 134 \right) = 0 . 27 \text { cm }\]
APPEARS IN
संबंधित प्रश्न
A hollow sphere filled with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
The time period of a particle in simple harmonic motion is equal to the time between consecutive appearances of the particle at a particular point in its motion. This point is
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
Figure represents two simple harmonic motions.
The parameter which has different values in the two motions is

The average energy in one time period in simple harmonic motion is
A pendulum clock that keeps correct time on the earth is taken to the moon. It will run
A pendulum clock keeping correct time is taken to high altitudes,
Select the correct statements.
(a) A simple harmonic motion is necessarily periodic.
(b) A simple harmonic motion is necessarily oscillatory.
(c) An oscillatory motion is necessarily periodic.
(d) A periodic motion is necessarily oscillatory.
The motion of a torsional pendulum is
(a) periodic
(b) oscillatory
(c) simple harmonic
(d) angular simple harmonic
For a particle executing simple harmonic motion, the acceleration is proportional to
The pendulum of a certain clock has time period 2.04 s. How fast or slow does the clock run during 24 hours?
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s2?
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.
Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.
Consider the Earth as a homogeneous sphere of radius R and a straight hole is bored in it through its centre. Show that a particle dropped into the hole will execute a simple harmonic motion such that its time period is
T = `2π sqrt("R"/"g")`
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
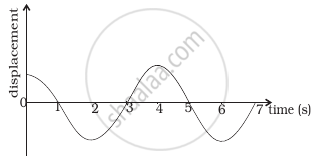
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
A body having specific charge 8 µC/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally toward the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be ______ s.

