Advertisements
Advertisements
प्रश्न
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
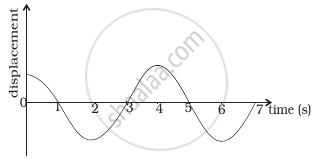
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
उत्तर
b and d
Explanation:
It is clear from the curve that points corresponding to t = 2s and t = 6s are separated by a distance belonging to one time period. Hence, these points must be in the same phase.
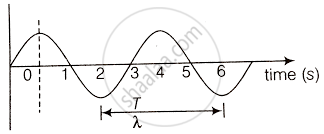
Similarly. points belonging to t = 1s and t = 5s are at a separation of one time period, hence must be in phase.
APPEARS IN
संबंधित प्रश्न
A pendulum clock keeping correct time is taken to high altitudes,
In a simple harmonic motion
(a) the maximum potential energy equals the maximum kinetic energy
(b) the minimum potential energy equals the minimum kinetic energy
(c) the minimum potential energy equals the maximum kinetic energy
(d) the maximum potential energy equals the minimum kinetic energy
A pendulum clock giving correct time at a place where g = 9.800 m/s2 is taken to another place where it loses 24 seconds during 24 hours. Find the value of g at this new place.
A simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator (a) is going up with and acceleration a0(b) is going down with an acceleration a0 and (c) is moving with a uniform velocity.
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is 3.0 cm and that of the second is 4.0 cm. Find the resultant amplitude if the phase difference between the motions is (a) 0°, (b) 60°, (c) 90°.
A particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45° with the X-axis. The two motions are given by x = x0 sin ωt and s = s0 sin ωt. Find the amplitude of the resultant motion.
State the laws of the simple pendulum?
Consider a simple pendulum of length l = 0.9 m which is properly placed on a trolley rolling down on a inclined plane which is at θ = 45° with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.
Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is ______.
- simple harmonic motion.
- non-periodic motion.
- periodic motion.
- periodic but not S.H.M.
