Advertisements
Advertisements
प्रश्न
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
पर्याय
not simple harmonic
simple harmonic with amplitude A + B
simple harmonic with amplitude (A + B)/2
simple harmonic with amplitude
उत्तर
simple harmonic with amplitude \[\sqrt{A^2 + B^2}\]
x = A sin ωt + B cos ωt ...(1)
\[\text { Acceleration }, \]
\[ a = \frac{\text {d}^2 x}{\text {dt}^2} = \frac{\text {d}^2}{\text{dt}^2}(\text {A}\sin\omega t + \text {B} \cos \omega t)\]
\[ = \frac{\text{d}}{\text {dt}}(\text { A }\omega \cos \omega t - \text { B }\omega \sin \omega t) \]
\[ = - \text { A } \omega^2 \text { sin }\omega t - \text { B }\omega^2 \cos \omega t \]
\[ = - \omega^2 (\text { A }\sin \omega t + \text { B }\cos \omega t )\]
\[ = - \omega^2 x\]
For a body to undergo simple harmonic motion,
acceleration, a =\[-\] kx. ...(2)
Therefore, from the equations (1) and (2), it can be seen that the given body undergoes simple harmonic motion with amplitude, A
\[= \sqrt{A^2 + B^2}\]
APPEARS IN
संबंधित प्रश्न
Assuming the expression for displacement of a particle starting from extreme position, explain graphically the variation of velocity and acceleration w.r.t. time.
A particle executes simple harmonic motion Let P be a point near the mean position and Q be a point near an extreme. The speed of the particle at P is larger than the speed at Q. Still the particle crosses Pand Q equal number of times in a given time interval. Does it make you unhappy?
The energy of system in simple harmonic motion is given by \[E = \frac{1}{2}m \omega^2 A^2 .\] Which of the following two statements is more appropriate?
(A) The energy is increased because the amplitude is increased.
(B) The amplitude is increased because the energy is increased.
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The displacement of a particle in simple harmonic motion in one time period is
The displacement of a particle is given by \[\overrightarrow{r} = A\left( \overrightarrow{i} \cos\omega t + \overrightarrow{j} \sin\omega t \right) .\] The motion of the particle is
A pendulum clock keeping correct time is taken to high altitudes,
A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s2?
A small block oscillates back and forth on a smooth concave surface of radius R ib Figure . Find the time period of small oscillation.
A simple pendulum of length 40 cm is taken inside a deep mine. Assume for the time being that the mine is 1600 km deep. Calculate the time period of the pendulum there. Radius of the earth = 6400 km.
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the road.
A particle is subjected to two simple harmonic motions given by x1 = 2.0 sin (100π t) and x2 = 2.0 sin (120 π t + π/3), where x is in centimeter and t in second. Find the displacement of the particle at (a) t = 0.0125, (b) t = 0.025.
A particle executing SHM crosses points A and B with the same velocity. Having taken 3 s in passing from A to B, it returns to B after another 3 s. The time period is ____________.
Define the frequency of simple harmonic motion.
A simple harmonic motion is given by, x = 2.4 sin ( 4πt). If distances are expressed in cm and time in seconds, the amplitude and frequency of S.H.M. are respectively,
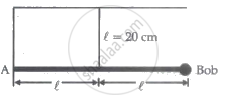
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)