Advertisements
Advertisements
प्रश्न
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
पर्याय
vmax
0
between 0 and vmax
between 0 and −vmax
उत्तर
vmax
Because the time period of a simple harmonic motion is defined as the time taken to complete one oscillation.
APPEARS IN
संबंधित प्रश्न
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
A particle executing simple harmonic motion comes to rest at the extreme positions. Is the resultant force on the particle zero at these positions according to Newton's first law?
A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on a horizontal plane move in a sample harmonic motion?
It is proposed to move a particle in simple harmonic motion on a rough horizontal surface by applying an external force along the line of motion. Sketch the graph of the applied force against the position of the particle. Note that the applied force has two values for a given position depending on whether the particle is moving in positive or negative direction.
Can the potential energy in a simple harmonic motion be negative? Will it be so if we choose zero potential energy at some point other than the mean position?
The motion of a torsional pendulum is
(a) periodic
(b) oscillatory
(c) simple harmonic
(d) angular simple harmonic
A particle moves on the X-axis according to the equation x = x0 sin2 ωt. The motion is simple harmonic
Which of the following will change the time period as they are taken to moon?
(a) A simple pendulum
(b) A physical pendulum
(c) A torsional pendulum
(d) A spring-mass system
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
A particle is subjected to two simple harmonic motions, one along the X-axis and the other on a line making an angle of 45° with the X-axis. The two motions are given by x = x0 sin ωt and s = s0 sin ωt. Find the amplitude of the resultant motion.
In a simple harmonic oscillation, the acceleration against displacement for one complete oscillation will be __________.
The length of a second’s pendulum on the surface of the Earth is 0.9 m. The length of the same pendulum on the surface of planet X such that the acceleration of the planet X is n times greater than the Earth is
A simple pendulum is suspended from the roof of a school bus which moves in a horizontal direction with an acceleration a, then the time period is
Define the time period of simple harmonic motion.
Define the frequency of simple harmonic motion.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______.
A spring is stretched by 5 cm by a force of 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is ______
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
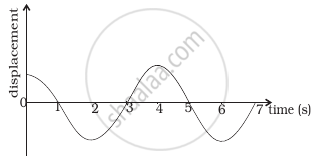
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
