Advertisements
Advertisements
प्रश्न
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
उत्तर
\[\frac{18}{100} = 0 . 18 m = 0 . 2 m\]
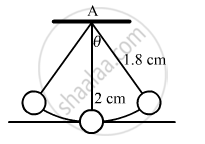
Let I be the moment of inertia and \[\omega\] be the angular speed.
Using the energy equation, we can write:
\[mgl(1 - \cos \theta) + \frac{1}{2}I \omega^2 = \text { constant }\]
\[mg\left( 0 . 20 \right) \left( 1 - \cos \theta \right) + \frac{1}{2}I \omega^2 = C . . . \left( 1 \right)\]
\[\text { Moment of inertia about the point of suspension A is given by, } \]
\[I = \frac{2}{3}m r^2 + m l^2 \]
\[\text { Substituting the value of l in the above equation, we get: }\]
\[I = \frac{2}{3}m \left( 0 . 02 \right)^2 + m \left( 0 . 2 \right)^2 \]
\[ = \frac{2}{3}m\left( 0 . 0004 \right) + m\left( 0 . 04 \right)\]
\[ = m\left[ \frac{0 . 0008}{3} + 0 . 04 \right]\]
\[ = m\left( \frac{0 . 1208}{3} \right)\]
On substituting the value of I in equation (1) and differentiating it, we get:
\[\frac{d}{dt}\left[ mg \left( 0 . 2 \right) \left( 1 - \cos \theta \right) + \frac{1}{2}\frac{0 . 1208}{3}m \omega^2 \right] = \frac{d}{dt}\left( c \right)\]
\[ \Rightarrow mg\left( 0 . 2 \right)\sin\theta\frac{d\theta}{dt} + \frac{1}{2}\left( \frac{0 . 1208}{3} \right)m \times 2\omega\frac{d\omega}{dt} = 0 \]
\[ \Rightarrow 2\sin \theta = \frac{0 . 1208}{3}\alpha \left[ \text { because }, g = 10 m/ s^2 \right]\]
\[ \Rightarrow \frac{\alpha}{\theta} = \frac{6}{0 . 1208}\]
\[ \Rightarrow \omega^2 = 49 . 66\]
\[ \Rightarrow \omega = 7 . 04\]
\[\text { Thus, time period }\left( T \right) \text { will be: }\]
\[T = \frac{2\pi}{\omega} = 0 . 89 s\]
For a simple pendulum, time period (T) is given by,
% change in the value of time period = \[\frac{0 . 89 - 0 . 86}{0 . 89} \times 100 = 0 . 3\]
APPEARS IN
संबंधित प्रश्न
In a damped harmonic oscillator, periodic oscillations have _______ amplitude.
(A) gradually increasing
(B) suddenly increasing
(C) suddenly decreasing
(D) gradually decreasing
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate:
a) Angular frequency
b) frequency of vibration.
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on a horizontal plane move in a sample harmonic motion?
The force acting on a particle moving along X-axis is F = −k(x − vo t) where k is a positive constant. An observer moving at a constant velocity v0 along the X-axis looks at the particle. What kind of motion does he find for the particle?
The displacement of a particle in simple harmonic motion in one time period is
The distance moved by a particle in simple harmonic motion in one time period is
A pendulum clock keeping correct time is taken to high altitudes,
The motion of a torsional pendulum is
(a) periodic
(b) oscillatory
(c) simple harmonic
(d) angular simple harmonic
Which of the following quantities are always positive in a simple harmonic motion?
In a simple harmonic motion
(a) the maximum potential energy equals the maximum kinetic energy
(b) the minimum potential energy equals the minimum kinetic energy
(c) the minimum potential energy equals the maximum kinetic energy
(d) the maximum potential energy equals the minimum kinetic energy
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
A simple pendulum of length l is suspended from the ceiling of a car moving with a speed v on a circular horizontal road of radius r. (a) Find the tension in the string when it is at rest with respect to the car. (b) Find the time period of small oscillation.
What is an epoch?
Consider two simple harmonic motion along the x and y-axis having the same frequencies but different amplitudes as x = A sin (ωt + φ) (along x-axis) and y = B sin ωt (along y-axis). Then show that
`"x"^2/"A"^2 + "y"^2/"B"^2 - (2"xy")/"AB" cos φ = sin^2 φ`
and also discuss the special cases when
- φ = 0
- φ = π
- φ = `π/2`
- φ = `π/2` and A = B
- φ = `π/4`
Note: when a particle is subjected to two simple harmonic motions at right angle to each other the particle may move along different paths. Such paths are called Lissajous figures.
A simple harmonic motion is given by, x = 2.4 sin ( 4πt). If distances are expressed in cm and time in seconds, the amplitude and frequency of S.H.M. are respectively,
A body oscillates with SHM according to the equation x = 5 cos `(2π"t" + π/4)`. Its instantaneous displacement at t = 1 sec is:
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
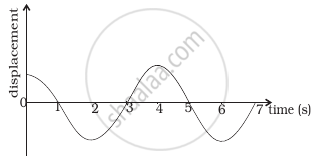
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
A body having specific charge 8 µC/g is resting on a frictionless plane at a distance 10 cm from the wall (as shown in the figure). It starts moving towards the wall when a uniform electric field of 100 V/m is applied horizontally toward the wall. If the collision of the body with the wall is perfectly elastic, then the time period of the motion will be ______ s.

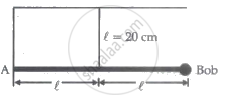
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)