Advertisements
Advertisements
प्रश्न
A hollow sphere of radius 2 cm is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum?
Advertisements
उत्तर
\[\frac{18}{100} = 0 . 18 m = 0 . 2 m\]
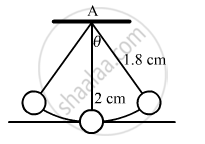
Let I be the moment of inertia and \[\omega\] be the angular speed.
Using the energy equation, we can write:
\[mgl(1 - \cos \theta) + \frac{1}{2}I \omega^2 = \text { constant }\]
\[mg\left( 0 . 20 \right) \left( 1 - \cos \theta \right) + \frac{1}{2}I \omega^2 = C . . . \left( 1 \right)\]
\[\text { Moment of inertia about the point of suspension A is given by, } \]
\[I = \frac{2}{3}m r^2 + m l^2 \]
\[\text { Substituting the value of l in the above equation, we get: }\]
\[I = \frac{2}{3}m \left( 0 . 02 \right)^2 + m \left( 0 . 2 \right)^2 \]
\[ = \frac{2}{3}m\left( 0 . 0004 \right) + m\left( 0 . 04 \right)\]
\[ = m\left[ \frac{0 . 0008}{3} + 0 . 04 \right]\]
\[ = m\left( \frac{0 . 1208}{3} \right)\]
On substituting the value of I in equation (1) and differentiating it, we get:
\[\frac{d}{dt}\left[ mg \left( 0 . 2 \right) \left( 1 - \cos \theta \right) + \frac{1}{2}\frac{0 . 1208}{3}m \omega^2 \right] = \frac{d}{dt}\left( c \right)\]
\[ \Rightarrow mg\left( 0 . 2 \right)\sin\theta\frac{d\theta}{dt} + \frac{1}{2}\left( \frac{0 . 1208}{3} \right)m \times 2\omega\frac{d\omega}{dt} = 0 \]
\[ \Rightarrow 2\sin \theta = \frac{0 . 1208}{3}\alpha \left[ \text { because }, g = 10 m/ s^2 \right]\]
\[ \Rightarrow \frac{\alpha}{\theta} = \frac{6}{0 . 1208}\]
\[ \Rightarrow \omega^2 = 49 . 66\]
\[ \Rightarrow \omega = 7 . 04\]
\[\text { Thus, time period }\left( T \right) \text { will be: }\]
\[T = \frac{2\pi}{\omega} = 0 . 89 s\]
For a simple pendulum, time period (T) is given by,
% change in the value of time period = \[\frac{0 . 89 - 0 . 86}{0 . 89} \times 100 = 0 . 3\]
APPEARS IN
संबंधित प्रश्न
A particle executes S.H.M. with a period of 10 seconds. Find the time in which its potential energy will be half of its total energy.
A body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate:
a) Angular frequency
b) frequency of vibration.
A student says that he had applied a force \[F = - k\sqrt{x}\] on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he was worked only with positive x and no other force acted on the particle.
The time period of a particle in simple harmonic motion is equal to the smallest time between the particle acquiring a particular velocity \[\vec{v}\] . The value of v is
The motion of a particle is given by x = A sin ωt + B cos ωt. The motion of the particle is
The average energy in one time period in simple harmonic motion is
A wall clock uses a vertical spring-mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
A pendulum clock keeping correct time is taken to high altitudes,
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
Which of the following quantities are always positive in a simple harmonic motion?
A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
A small block oscillates back and forth on a smooth concave surface of radius R in Figure. Find the time period of small oscillation.
Assume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. (a) Find the gravitational force exerted by the earth on a particle of mass mplaced in the tunnel at a distance x from the centre of the tunnel. (b) Find the component of this force along the tunnel and perpendicular to the tunnel. (c) Find the normal force exerted by the wall on the particle. (d) Find the resultant force on the particle. (e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
Define the frequency of simple harmonic motion.
Write short notes on two springs connected in parallel.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
Displacement vs. time curve for a particle executing S.H.M. is shown in figure. Choose the correct statements.
- Phase of the oscillator is same at t = 0 s and t = 2s.
- Phase of the oscillator is same at t = 2 s and t = 6s.
- Phase of the oscillator is same at t = 1 s and t = 7s.
- Phase of the oscillator is same at t = 1 s and t = 5s.
A container consist of hemispherical shell of radius 'r ' and cylindrical shell of height 'h' radius of same material and thickness. The maximum value h/r so that container remain stable equilibrium in the position shown (neglect friction) is ______.
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20 cm, fixed at its midpoint. The bob is displaced slightly, perpendicular to the plane of the rod and string. The period of small oscillations of the system in the form `(pix)/10` is ______ sec. and the value of x is ______.
(g = 10 m/s2)
