Advertisements
Advertisements
प्रश्न
Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower point is ______.
- simple harmonic motion.
- non-periodic motion.
- periodic motion.
- periodic but not S.H.M.
उत्तर
a and c
Explanation:
For small angular displacement, the situation is shown in the figure. Only one restoring force creates motion in a ball inside the bowl.
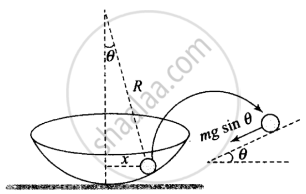
F = – mg sin θ
As θ is small, sin θ = θ
So, `ma = - mg x/R`
or a = `- (g/R)x`
⇒ a ∝ – x
So, the motion of the ball is S.H.M and periodic.
APPEARS IN
संबंधित प्रश्न
A particle in S.H.M. has a period of 2 seconds and amplitude of 10 cm. Calculate the acceleration when it is at 4 cm from its positive extreme position.
State the differential equation of linear simple harmonic motion.
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
Can a pendulum clock be used in an earth-satellite?
Which of the following quantities are always negative in a simple harmonic motion?
(a) \[\vec{F} . \vec{a} .\]
(b) \[\vec{v} . \vec{r} .\]
(c) \[\vec{a} . \vec{r} .\]
(d)\[\vec{F} . \vec{r} .\]
A particle executes simple harmonic motion with an amplitude of 10 cm and time period 6 s. At t = 0 it is at position x = 5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t = 4 s.
A pendulum having time period equal to two seconds is called a seconds pendulum. Those used in pendulum clocks are of this type. Find the length of a second pendulum at a place where g = π2 m/s2.
Describe Simple Harmonic Motion as a projection of uniform circular motion.
The velocities of a particle in SHM at positions x1 and x2 are v1 and v2 respectively, its time period will be ______.
