Advertisements
Advertisements
प्रश्न
Define the time period of simple harmonic motion.
उत्तर
Time period: The time period is defined as the time taken by a particle to complete one oscillation. It is usually denoted by T. For one complete revolution, the time taken is t = T, therefore,
`ω"T"` = 2π ⇒ T = `(2π)/ω`
APPEARS IN
संबंधित प्रश्न
The average displacement over a period of S.H.M. is ______.
(A = amplitude of S.H.M.)
Can simple harmonic motion take place in a non-inertial frame? If yes, should the ratio of the force applied with the displacement be constant?
A particle moves on the X-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude
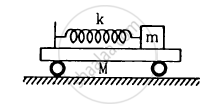
All the surfaces shown in figure are frictionless. The mass of the care is M, that of the block is m and the spring has spring constant k. Initially the car and the block are at rest and the spring is stretched through a length x0 when the system is released. (a) Find the amplitudes of the simple harmonic motion of the block and of the care as seen from the road. (b) Find the time period(s) of the two simple harmonic motions.
A simple pendulum is constructed by hanging a heavy ball by a 5.0 m long string. It undergoes small oscillations. (a) How many oscillations does it make per second? (b) What will be the frequency if the system is taken on the moon where acceleration due to gravitation of the moon is 1.67 m/s2?
Three simple harmonic motions of equal amplitude A and equal time periods in the same direction combine. The phase of the second motion is 60° ahead of the first and the phase of the third motion is 60° ahead of the second. Find the amplitude of the resultant motion.
What is meant by simple harmonic oscillation? Give examples and explain why every simple harmonic motion is a periodic motion whereas the converse need not be true.
The displacement of a particle is represented by the equation y = sin3ωt. The motion is ______.
The displacement of a particle varies with time according to the relation y = a sin ωt + b cos ωt.
What is the ratio of maxmimum acceleration to the maximum velocity of a simple harmonic oscillator?
