Advertisements
Advertisements
Question
What is meant by simple harmonic oscillation? Give examples and explain why every simple harmonic motion is a periodic motion whereas the converse need not be true.
Solution
Simple harmonic motion is a special type of oscillatory motion in which the acceleration or force on the particle is directly proportional to its displacement from a fixed point and is always directed towards that fixed point. In one dimensional case, let x be the displacement of the particle and ax be the acceleration of the particle, then
ax ∝ x .................(1)
ax = −bx ...............(2)
where b is a constant which measures acceleration per unit displacement and dimensionally it is equal to T-2.
By multiplying by the mass of the particle on both sides of equation (1) and from Newton’s second law, the force is
Fx = −kx ….........(3)
where k is a force constant which is defined as force per unit length. The negative sign indicates that displacement and force (or acceleration) are in opposite directions. This means that when the displacement of the particle is taken towards the right of equilibrium position (x takes positive value), the force (or acceleration) will point towards equilibrium (towards left) and similarly, when the displacement of the particle is taken towards left of equilibrium position (x takes negative value), the force (or acceleration) will point towards equilibrium (towards right). This type of force is known as restoring force because it always directs the particle executing simple harmonic motion to restore to its original (equilibrium or mean) position. This force (restoring force) is central and attractive whose center of attraction is the equilibrium position.
In order to represent in two or three dimensions, we can write using vector notation
`vec"F" = -"k"vec("r")` ...(4)
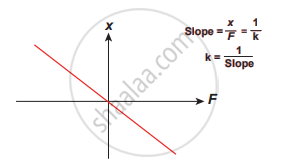
where `vec"r"` is the displacement of the particle from the chosen origin. Note that the force and displacement have a linear relationship. This means that the exponent of force `vec"F"` and the exponent of displacement `vec"r"` are unity. The sketch between cause (magnitude of force `vec|"F"|`) and effect (magnitude of displacement `vec|"r"|`) is a straight line passing through the second and fourth quadrant.
By measuring slope `1/"k"`, one can find the numerical value of force constant k.
APPEARS IN
RELATED QUESTIONS
Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
The distance moved by a particle in simple harmonic motion in one time period is
Figure represents two simple harmonic motions.
The parameter which has different values in the two motions is

A wall clock uses a vertical spring-mass system to measure the time. Each time the mass reaches an extreme position, the clock advances by a second. The clock gives correct time at the equator. If the clock is taken to the poles it will
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point, a distance h directly above the tunnel. The motion of the particle as seen from the earth is
(a) simple harmonic
(b) parabolic
(c) on a straight line
(d) periodic
The angle made by the string of a simple pendulum with the vertical depends on time as \[\theta = \frac{\pi}{90} \sin \left[ \left( \pi s^{- 1} \right)t \right]\] .Find the length of the pendulum if g = π2 m2.
A simple pendulum of length 1 feet suspended from the ceiling of an elevator takes π/3 seconds to complete one oscillation. Find the acceleration of the elevator.
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 20 and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π2 m/s2.
A uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
If the inertial mass and gravitational mass of the simple pendulum of length l are not equal, then the time period of the simple pendulum is
