Question

A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude 2⁰ and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it is at an extreme position. Take g = π² m/s².

Answer 1

It is given that:
Time period of oscillation, T = 2 s
Acceleration due to gravity, g =\[\pi^2\]ms⁻²

^{Let I be the moment of inertia of the circular wire having mass m and radius r.}

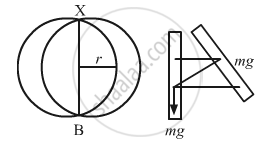
^{(a) Time period of compound pendulum \[\left( T \right)\] is given by ,}

^{\[T = 2\sqrt{\frac{I}{mgl}} = 2\sqrt{\frac{I}{mgr}}\]}

^{\[\left( \because l = r \right)\] ...(1)  
Moment of inertia about the point of suspension  is calculated as,
I = mr2 + mr2 = 2mr2
On substituting the value of moment of inertia I in equation (1), we get:}

\[T = 2\pi\sqrt{\frac{2m r^2}{mgr}} = 2\pi\sqrt{\frac{2r}{g}}\] 

\[ \Rightarrow \frac{2}{2\pi} = \sqrt{\frac{2r}{g}}\] 

\[ \Rightarrow \frac{2r}{g} = \frac{1}{\pi^2}\] 

\[ \Rightarrow r = \frac{g}{2 \pi^2}\] 

\[           = 0 . 5  m = 50  cm\]

(b) From the energy equation, we have:

\[\frac{1}{2}I \omega^2  - 0 = mgr  \left( 1 - \cos  \theta \right)\] 

\[\frac{1}{2}I \omega^2  - 0 = mgr  \left( 1 - \cos  2^\circ \right)\]

\[\Rightarrow \left( \frac{1}{2} \right)2m r^2  \cdot  \omega^2  = mgr\left( 1 - \cos  2^\circ\right)                    \left( \because I = 2m r^2 \right)\] 

\[ \Rightarrow  \omega^2  = \frac{g}{r}\left( 1 - \cos  2^\circ\right)\] 

\[\text { On  substituing  the  value  of  g  and  r  in  the  above  equation,   we  get:}\] \[\omega = 0 . 11  rad/s\] 

\[ \Rightarrow v = \omega \times 2r = 11   {\text { cms }}^{- 1}\]

(c) The acceleration is found to be centripetal at the extreme position.
    Centripetal acceleration at the extreme position \[\left( a_n \right)\] is given by,
    a_n = ω²(2r) = (0.11) × 100 = 12 cm/s²
    The direction of a_n is towards the point of suspension.

(d) The particle has zero centripetal acceleration at the extreme position. However, the particle will still have acceleration due to the S.H.M.
 Angular frequency \[\left( \omega \right)\] is given by ,

\[\omega = \frac{2\pi}{T}\] 

\[   = \frac{2\pi}{2} = 3 . 14\]

\[\therefore\] Angular Accelaration \[\left( a \right)\] at the extrame position is given as ,

\[\alpha =  \omega^2 \theta\] 

\[\alpha =  \omega^2 2^\circ=  \pi^2  \times \frac{2\pi}{180}\] 

\[   = \frac{2 \pi^3}{180}  \left[ 1^\circ= \frac{\pi}{180}\text { radian } \right]\]

Thus , tangential acceleration

\[= \alpha\left( 2r \right) = \left( \frac{2 \pi^3}{180} \right) \times 100\]

  = 34 cm/s²